Watberry Process Improvement
Overview
This is a slightly modified version of my final exam for my course in statistical methods for process improvement (STAT 435) at the University of Waterloo. This course taught a process improvement methodology called statistical engineering, related to but distinct from six sigma. The exam provided a simulation of a manufacturing process with a (randomized) problem which was causing excess variation in the process output. The goal was to diasgnose and then fix that problem using the statistical engineering methodology. I received the department's award for being the top-performing student in the class and I loved both the topic and the class itself, so I combined my analysis code with my written reports in Rmarkdown to provide a description of the analysis process.
The premise of the simulation is that the manufacturing process is an assembly process with 3 main steps. The process has variable inputs -- labelled x1 through x60 -- which vary randomly external to the process, and fixed inputs -- labelled z1 through z30 -- which can be set for the process. The output dimension of interest (called y300) can be measured at each step of the process, resulting in intermediate outputs y100 and y200 after steps 1 and 2, respectively. The the target for the output dimension is 0, with tolerances of \(\pm 10\). However, getting values closer to 0 can yield quality cost savings, so both reducing the absolute range of output values and reducing their standard deviation are goals of the improvement process. As in a real manufacturing setting, investigation and experimentation has a (well-defined) cost, as do the various solution approaches. The ultimate objective of the process is to change the process to obtain the biggest net cost savings per part, given a budget of $10,000 for the series of investigations.
This same simulation (with different parameters) was used throughout the course, but to save time for the exam, we were told that a series of initial examinations was performed ("the baseline") which found the process had excess variation, with a standard deviation of 5 and a range of output values (full extent of variation) from -12.5 to 12.5. It ruled out measurement as a possible contributor to the observed variation, and found that the dominant cause of process variation existed in the first process step of initial assembly. Variation did not exhibit a consistent time pattern, instead occuring part-to-part. In this first step, 5 components are combined in a prep area. Each component presents 3 significant varying inputs (x1 through x15), and the prep step itself has 10 significant varying inputs (x16 through x25). There are 6 fixed inputs which can be set in the prep step, which are labelled z1 through z6, and the output of the prep step is y100.
The statistical engineering process is divided into two steps: the diagnostic step, and the remedial step. In the diagnostic step, the process is characterized and the dominant cause(s) of process variation are determined. In the remedial step, variation reduction approaches are assessed, tested, and implemented. We start halfway through the diagnostic step, focused on the 25 varying inputs in the first step of the process.
Investigation 1 – y100 Baseline
Since the overall process baseline was already established and the process variation was deemed part-to-part, the plan for this investigation was to span a relatively small number of periods. This was chosen to be 3 days, with 4 blocks of observations in each shift, for a total of 36 blocks. With a goal of ~300 observations overall, 9 consecutive observations within each block gives 324 observations, with an associated cost of $324.
library(ggplot2)
baseline.data <- read.delim("y100-baseline.tsv")
baseline.data$shift <- as.factor(baseline.data$shift)
baseline.data$day <- as.factor(baseline.data$daycount)
baseline.data$shift.hour <- as.integer(baseline.data$shift)*8 + (baseline.data$daycount-1)*24 - 4Analysis
We can start with some summary statistics of the observations.
c(summary(baseline.data$y100), Std.Dev=sd(baseline.data$y100))## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -12.2500000 -2.0000000 0.6250000 0.8271605 3.7500000 12.5000000
## Std.Dev
## 4.5670346The data spans a range of -12.25 - 12.50, and have a standard deviation of 4.57. The mean is 0.827 and the median is 0.625, with the middle 50% of the data spanning the range -2 - 3.75. This is all quite close to the results from the initial baseline, suggesting the relationship between y100 and y300 may on average be close to 1:1.
We can further explore the data via a histogram. The data are somewhat normally distributed, and may exhibit a slight positive skew. Regardless, we can see how many values lie outside of the specification limits -10 to 10: calculating this, 3.7% of the data are outside of the specification limits.
ggplot(baseline.data) +
geom_histogram(aes(x=y100), data=baseline.data, bins=25, color="white") +
labs(title="Distribution of y100",
y="Frequency") +
theme(plot.title=element_text(hjust=0.5, face="bold"),
axis.title=element_text(size=12))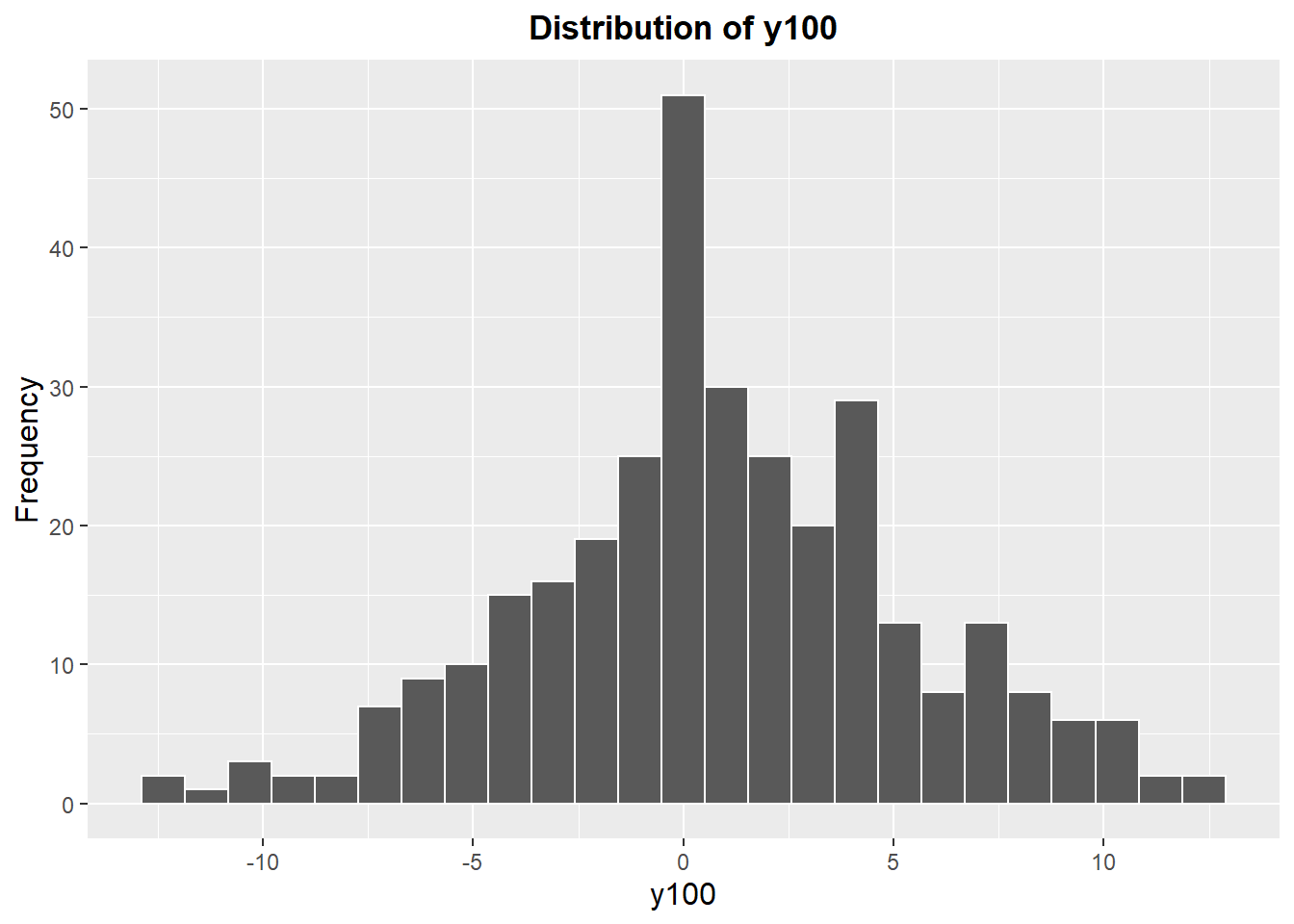
We can better confirm the distribution of the data via a quantile-quantile plot, shown below. The data appear to be quite normally distributed, with the observations not even particularly departing from the theoretical distribution at the tails.
ggplot(baseline.data) + geom_qq(aes(sample=y100), data=baseline.data) +
geom_qq_line(aes(sample=y100)) +
labs(title="Plot of observed y100 vs normal distribution\nby quantiles",
y="y100", x="Standard Normal") +
theme(plot.title=element_text(hjust=0.5, face="bold"),
axis.title=element_text(size=12))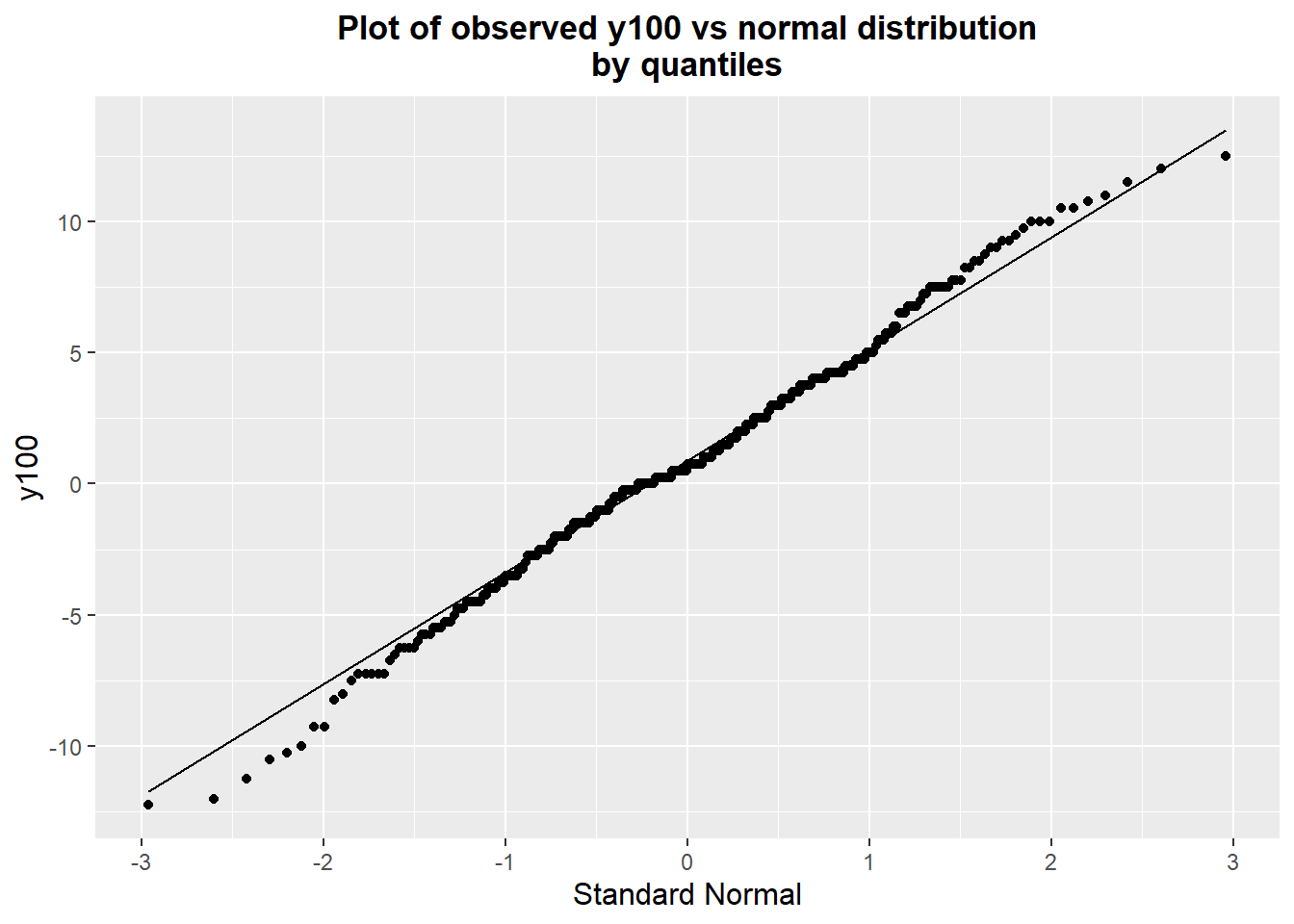
The most important visualization for understanding the process is a time series. The original baseline of the final output y300 showed a part-to-part time family -- very little of the variability appeared to be due to systematic variation on the scale of hours, shifts, or days. Because the dominant cause was hypothesized to act before the intermediate output y100, we expect it to have the same pattern. This is verified by the time series below. The blue points representing the hourly averages does not exhibit a great deal of variation. It has a standard deviation of 1.35, compared to the overall process standard deviation of 4.57.
baseline.summary.hour <- data.frame(hour=unique(baseline.data$partnum%/%60),
y100.mean=tapply(baseline.data$y100,
baseline.data$partnum%/%60,
mean),
y100.sd=tapply(baseline.data$y100,
baseline.data$partnum%/%60,
sd))
ggplot(baseline.data) +
geom_point(aes(x=partnum/60, y=y100), data=baseline.data,
color="#F06060", alpha=0.7, size=1) +
geom_point(aes(x=hour, y=y100.mean), data=baseline.summary.hour, color="#2030FF", size=2) +
geom_line(aes(x=hour, y=y100.mean), data=baseline.summary.hour, color="#2030FF") +
labs(title="Time series of y100 baseline",
x="Hour") +
scale_x_continuous(breaks=seq(0, max(baseline.data$partnum%/%60)+1, 8)) +
geom_hline(yintercept=max(baseline.data$y100)) +
geom_hline(yintercept=min(baseline.data$y100)) +
theme(plot.title=element_text(hjust=0.5, face="bold"),
axis.title=element_text(size=12))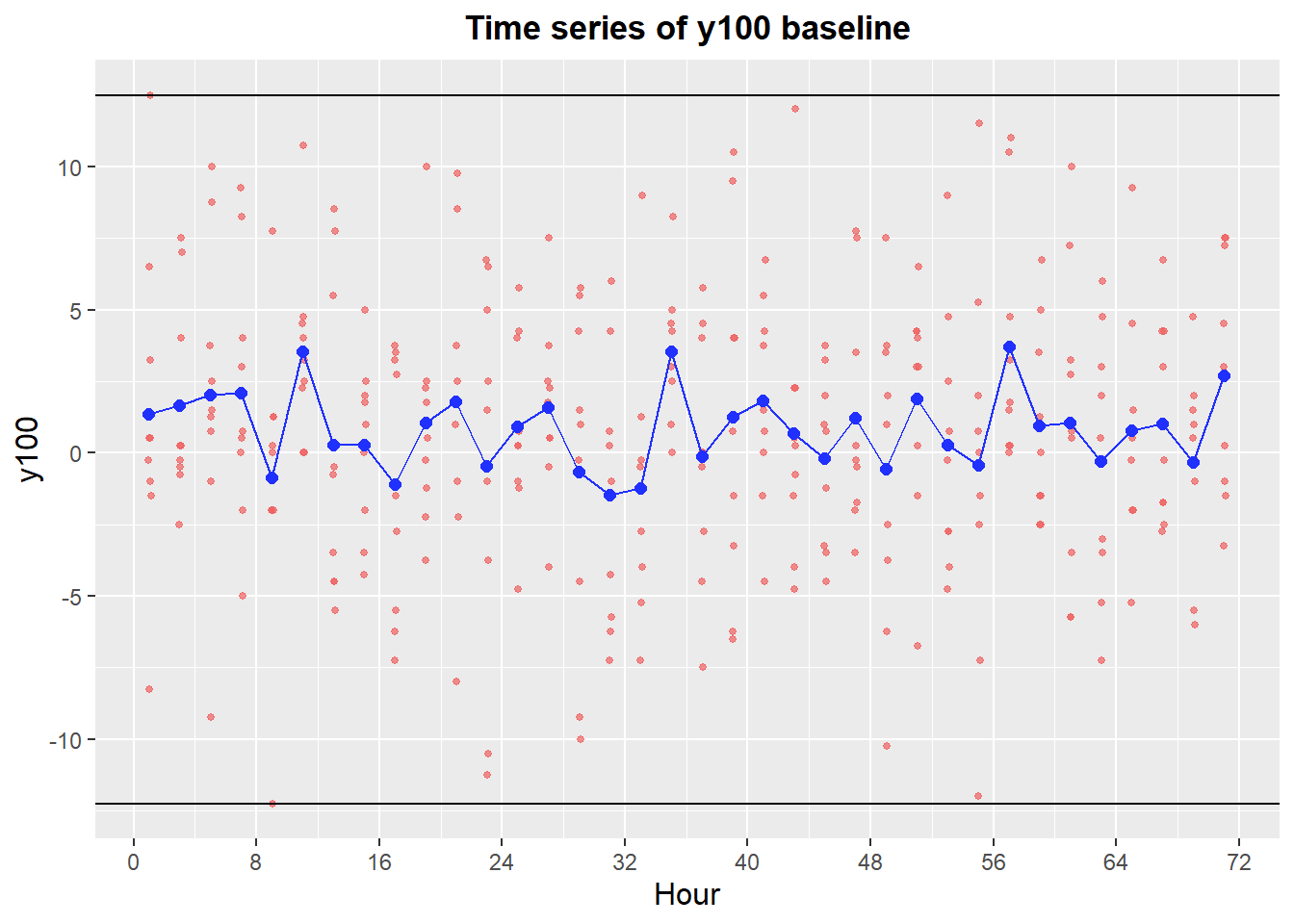
An ANOVA table of the data partitioned by day, then shift, then hour is shown below. We can see that at y100, the vast majority of variability occurs part-to-part - less than 10% of the total variation comes from longer time scales.
baseline.anova <- aov(y100 ~ day + as.factor(shift.hour) + as.factor(partnum%/%60),
data=baseline.data)
baseline.aov <- summary(baseline.anova)
baseline.aov## Df Sum Sq Mean Sq F value Pr(>F)
## day 2 8 3.769 0.176 0.839
## as.factor(shift.hour) 6 76 12.702 0.593 0.736
## as.factor(partnum%/%60) 27 489 18.123 0.847 0.688
## Residuals 288 6164 21.403baseline.aov[[1]][["Sum Sq"]]/sum(baseline.aov[[1]][["Sum Sq"]])## [1] 0.001118798 0.011312134 0.072631403 0.914937665We can look at the normality of the residuals; this is fairly important for the ANOVA F-test, but we're not particularly interested in the statistical conclusion of the ANOVA, just a sense of how variation breaks down by time. Both an examination of a quantile-quantile plot and a Shapiro-Wilk test of normality on the data show that the normality assumption seems fairly reasonable.
ggplot(baseline.data) + geom_qq(aes(sample=baseline.anova$residuals)) +
geom_qq_line(aes(sample=baseline.anova$residuals)) +
labs(title="Plot of y100 residuals vs normal distribution\nby quantiles",
y="y100", x="Standard Normal") +
theme(plot.title=element_text(hjust=0.5, face="bold"),
axis.title=element_text(size=12))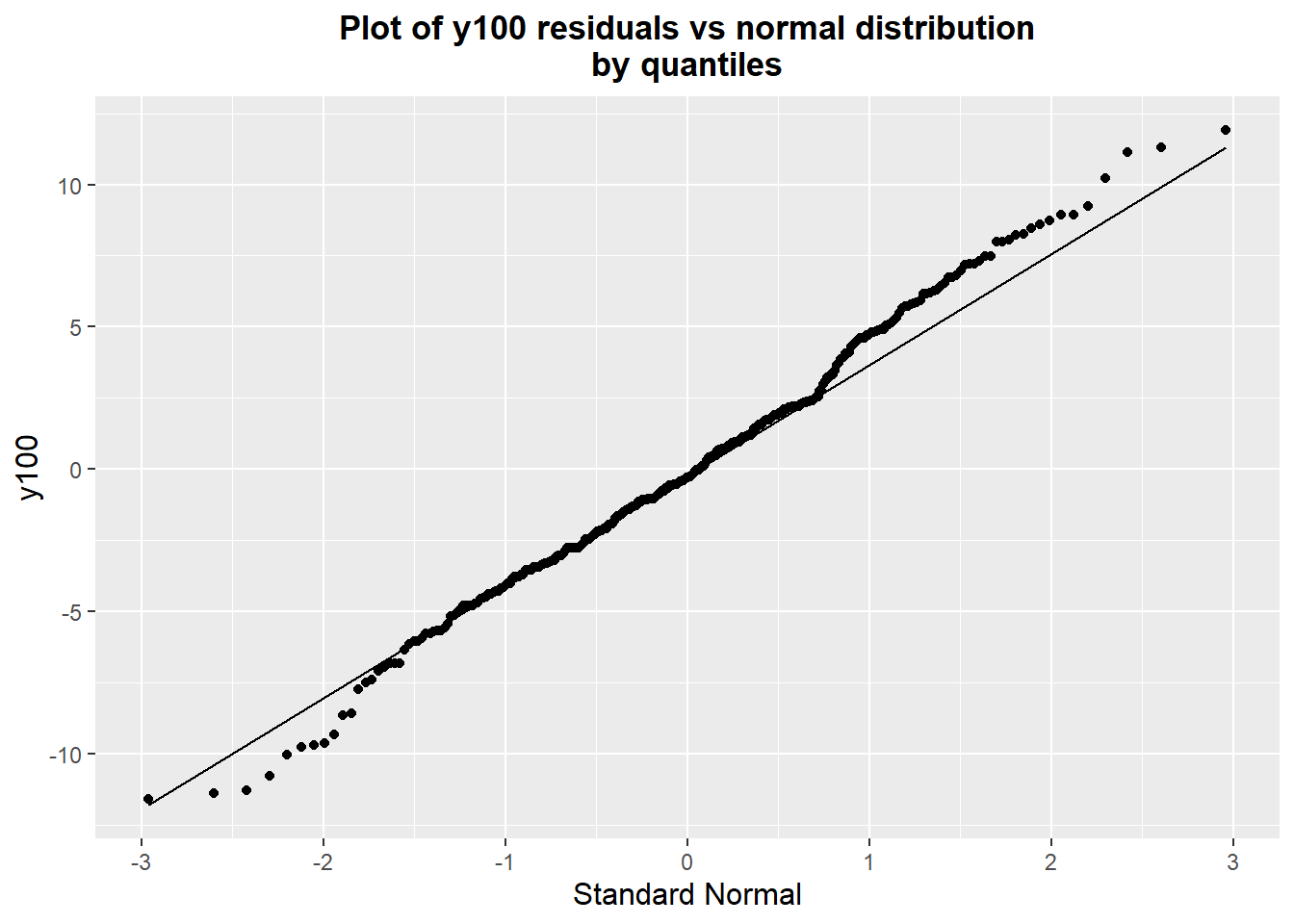
shapiro.test(baseline.anova$residuals)##
## Shapiro-Wilk normality test
##
## data: baseline.anova$residuals
## W = 0.99418, p-value = 0.2526Investigation 2 – Component Swap
Having determined that the dominant cause acts in step 100 or in the components, there are 25 varying inputs which could be the dominant cause of observed variation. These inputs are either a part of the input components or variables in step 100. At some point, we will have to measure individual inputs and observe their relationship with y100, but doing so with all 25 inputs would be very expensive. We want to take some action to narrow down our list before measuring individual inputs. Because the dominant cause is acting somewhere in the initial assembly step, we can make use of the assembly process to do this narrowing down, via a few experiments.
Disassembly-Reassembly Experiment
The first experiment is disassembly-reassembly: we take the assembly apart and put it back together with all the same components. If the variation is coming from the components which are going into the assembly, then reassembly should not significantly change the output. If instead the variation comes from something in the assembly process itself, we should see a large amount of variability in y100 for reassemblies of each "part". We can make use of the baseline we already observed; presumably, we've set aside the more extreme parts we measured in the baseline. To make it easier to observe the variability in the assembly process, we can use extreme parts from the baseline. If the dominant cause is in the assembly process, we would expect reassemblies to have y100 values following the same approximate normal distribution centered around 0. If not, the y100 values of the reassembled parts should be close to the extreme values we already measured. Observing extreme values of y100 (which match those observed in the baseline) would be extremely unlikely under the model where the dominant cause acts in the assembly process, so the identifying power of this investigation should be quite high.
We observed a full extent of variation in y100 of -12.25 to 12.50 in the baseline. Rather than choosing the most extreme points, I picked the closest points to \(\pm 10\), reasoning that the most extreme parts might have idiosyncracies that could complicate analysis. y100 values of \(\pm 10\) is still about two standard deviations away from the process center, and is expected to on average map to final output (y300) values of \(\pm 10\), which is more or less outside the process specification. These were obtained from our baseline file.
baseline.data <- read.delim("y100-baseline.tsv")
index.pos <- which.min(abs(baseline.data$y100-10))
index.neg <- which.min(abs(baseline.data$y100+10))
baseline.data[c(index.pos, index.neg),]The two closest parts were parts 306 and 1747 from the baseline, with y100 values of exactly +10 and -10. These were disassembled and reassembled three times each, giving 4 observations of assemblies using the same components.
reassembly.data <- read.delim("reassembly1.tsv")
colnames(reassembly.data) <- c("partnum", "y100")
reassembly.data <- rbind(reassembly.data,
baseline.data[c(index.pos, index.neg), c("partnum", "y100")])
reassembly.dataggplot(data=reassembly.data) + geom_point(aes(x=as.factor(partnum), y=y100)) +
labs(title="Plot of reassembly test results",
x="Part Number") +
theme(plot.title=element_text(hjust=0.5))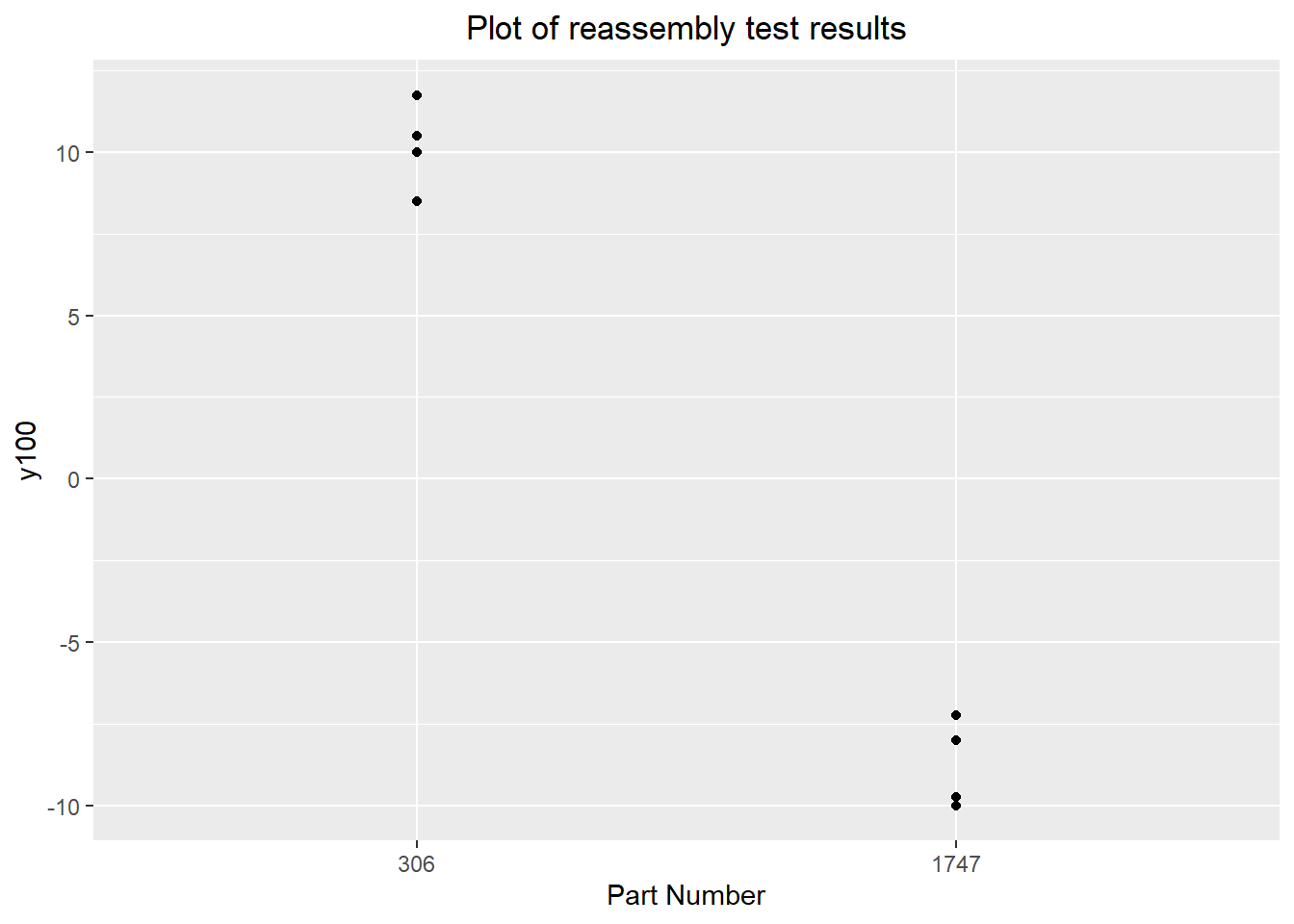
summary(aov(y100 ~ as.factor(partnum), data=reassembly.data))## Df Sum Sq Mean Sq F value Pr(>F)
## as.factor(partnum) 1 717.3 717.3 398.6 1.02e-06 ***
## Residuals 6 10.8 1.8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1These observations are consistent with the dominant cause lying in one of the components rather than the assembly process. This is confirmed statistically with the analysis of variance shown above. This means the investigation can be directed to the components rather than the assembly process (step 100). This narrows our list of suspect varying inputs to 15 -- 3 for each component.
Component Swap Analysis
Having established that the dominant cause is likely to lie in the components, we need a process to eliminate groups of suspect inputs. We can do this by component swap investigation, looking at how the components affect the output y100. If the dominant cause lies in some particular component, we would expect that swapping that component between two parts would result in the value of interest (y100) to more or less swap between the parts as well. We can use the same two parts, 306 and 1747. Having five different components going into each part and being able to only swap two components at once, we can start with swapping components A and B together.
swap1 <- data.frame(partnum=c(306,1747),
y100=c(-4.25, 6.5),
swap="A+B")
reassembly.data$swap <- "None"
full.data <- rbind(swap1, reassembly.data)
ggplot(data=full.data) + geom_point(aes(x=as.factor(partnum), y=y100, color=swap)) +
labs(title="Plot of Component Swap test Results",
x="Part Number") +
theme(plot.title=element_text(hjust=0.5)) +
scale_color_discrete(name="Components\nSwapped")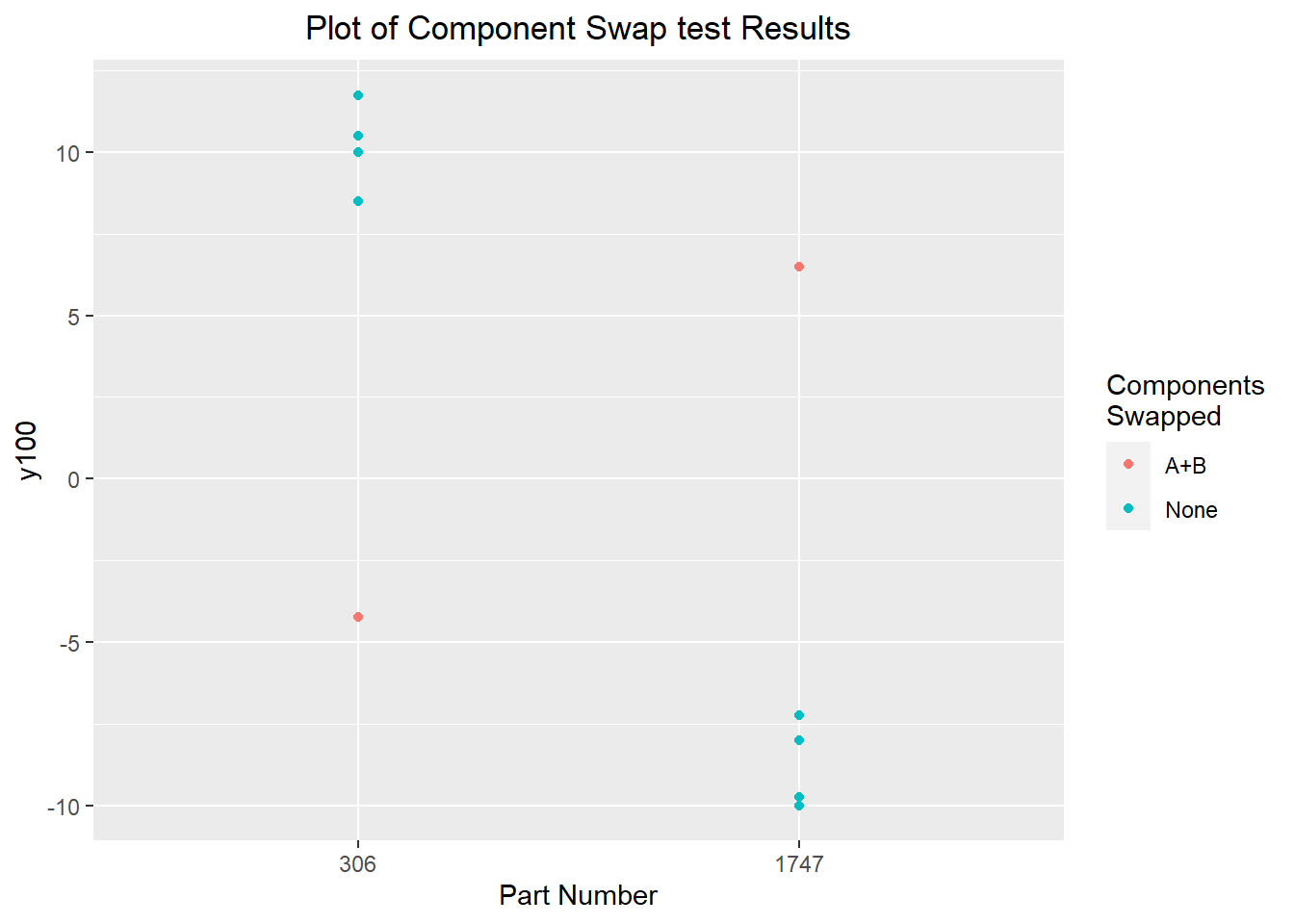
Swapping components A and B between the two parts, we see a substantial deviation from the pattern set by the disassembly-reassembly investigation. It's not quite a perfect flip for either part, with the parts with swapped components instead around 60% of the deviation from the process center that was seen in the original parts. This is explained by a sort of regression to the mean effect. We chose the original parts because they were extreme, and it's more likely than not that -- in addition to the dominant cause being extreme -- the other variables in the components acted to produce a more extreme result on average. When we swap components A and B, the unswapped components C, D, and E act to bias the observed y100 towards the original extreme.
Regardless, we see a very significant effect which indicates the dominant cause is in components A or B. The next step is to narrow it down further to one of the two components. Starting with component A, we see basically no difference between the parts with component A swapped and the reassemblies with the original components. Swapping component B, we see a significant difference, similar to the effect seen when components A and B were both swapped. The effect is slightly smaller for both parts; this might be a chance occurance from the measurement and reassembly variability, or it may be an effect of reversion to the mean.
swap2 <- data.frame(partnum=c(306,1747),
y100=c(13.5, -8.75),
swap="A")
swap3 <- data.frame(partnum=c(306,1747),
y100=c(-1, 5.25),
swap="B")
full.data <- rbind(swap1, swap2, swap3, reassembly.data)
ggplot(data=full.data) + geom_point(aes(x=as.factor(partnum), y=y100, color=swap, shape=swap)) +
labs(title="Plot of Component Swap test Results",
x="Part Number") +
theme(plot.title=element_text(hjust=0.5)) +
scale_color_discrete(name="Components\nSwapped") +
scale_shape_discrete(name="Components\nSwapped")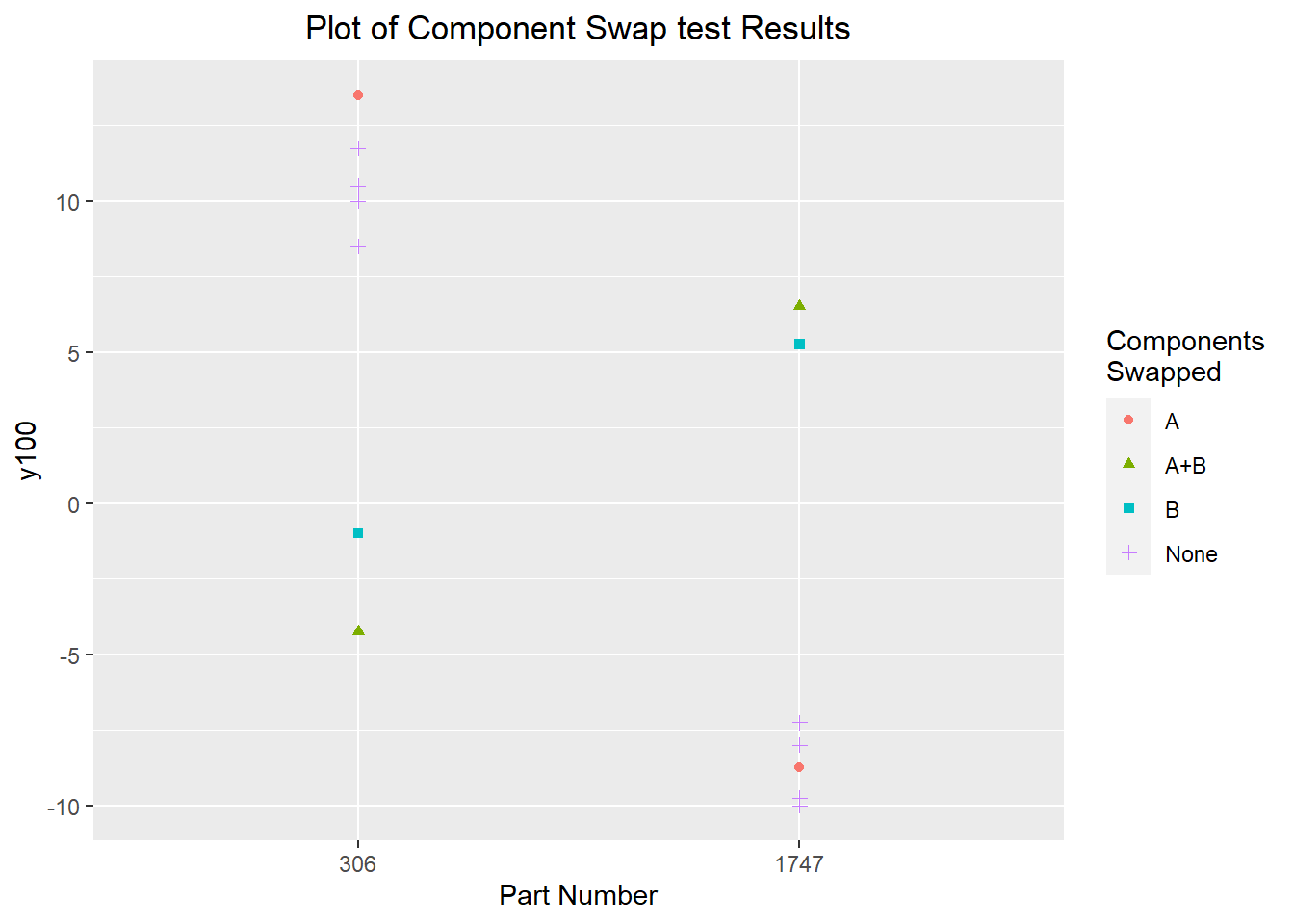
There was some suspicion in this conclusion, especially since the component swap result for part 306 was -1; very close to the process center and closer to halfway between the two parts' reassembly centres than to the values seen for part 1747. The expectation that there would be a strong flip, where the dominant cause basically determined whether a part was at the upper or lower extreme, which would be visible in the component swap. To rule out an interaction between the components or another effect, two more component swap investigations were performed with the remaining components: components C and D as a group, and component E. These component swap experiments produced very similar results to the original disassembly-reassembly experiments, as well as the component swap with component A. This was sufficient evidence to make component B the focus of future investigations. It seems likely that there is some interaction between the components, but the evidence seen is significant enough that controlling the effect of component B on its own seems to be a worthwhile endeavour.
swap.cd <- data.frame(partnum=c(306,1747),
y100=c(10.75, -6),
swap="C+D")
swap.e <- data.frame(partnum=c(306,1747),
y100=c(13.5, -8.75),
swap="E")
full.data <- rbind(swap1, swap2, swap3, swap.cd, swap.e, reassembly.data)
ggplot(data=full.data) + geom_point(aes(x=as.factor(partnum), y=y100, color=swap, shape=swap), position=position_jitter(0.05)) +
labs(title="Plot of Component Swap test Results",
x="Part Number") +
theme(plot.title=element_text(hjust=0.5)) +
scale_color_discrete(name="Components\nSwapped") +
scale_shape_discrete(name="Components\nSwapped")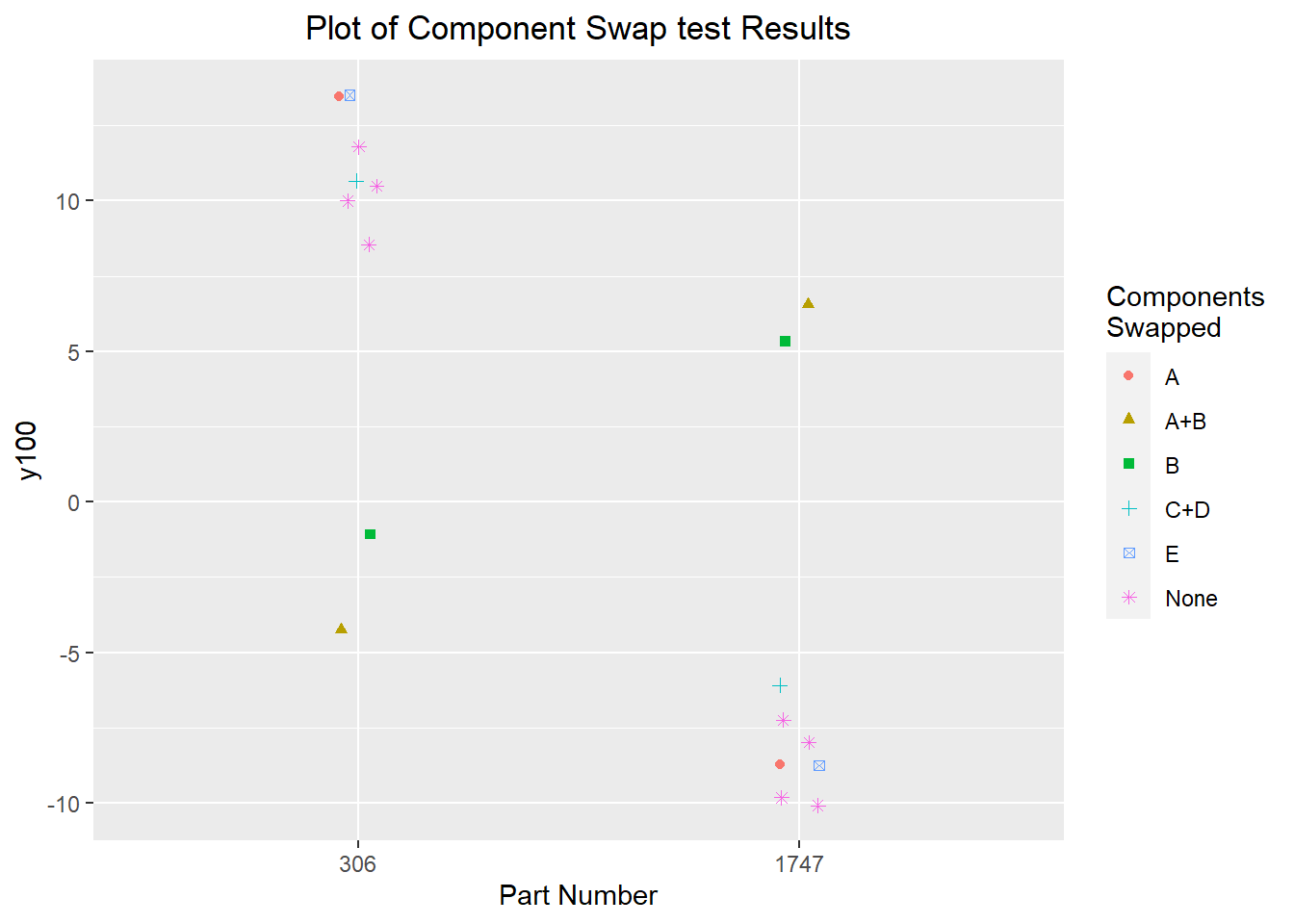
Investigation 3 – Group Comparisons
In the previous investigation, we determined the dominant cause is in component B of the assembly process, leaving us with only 3 suspect varying inputs. This is a small enough number that it's feasible to observe each input and its relationship with the output (or, in this case, the intermediate output y100). Because of the nature of the preassembly step (step 100), we can take the parts we observed in the baseline and retroactively measure the values of the varying inputs for the components (the component dimensions). This is quite useful, since we can focus our investigation on the extreme parts which we observed in the baseline. This is described in the statistical engineering algorithm as a "group comparisons" investigation, since we're looking at differences between two groups of parts (the upper and lower extremes).
Obtaining the max and min parts
To determine the parts to sample for the retrospective investigation, we can refer back to our histogram of the baseline data:
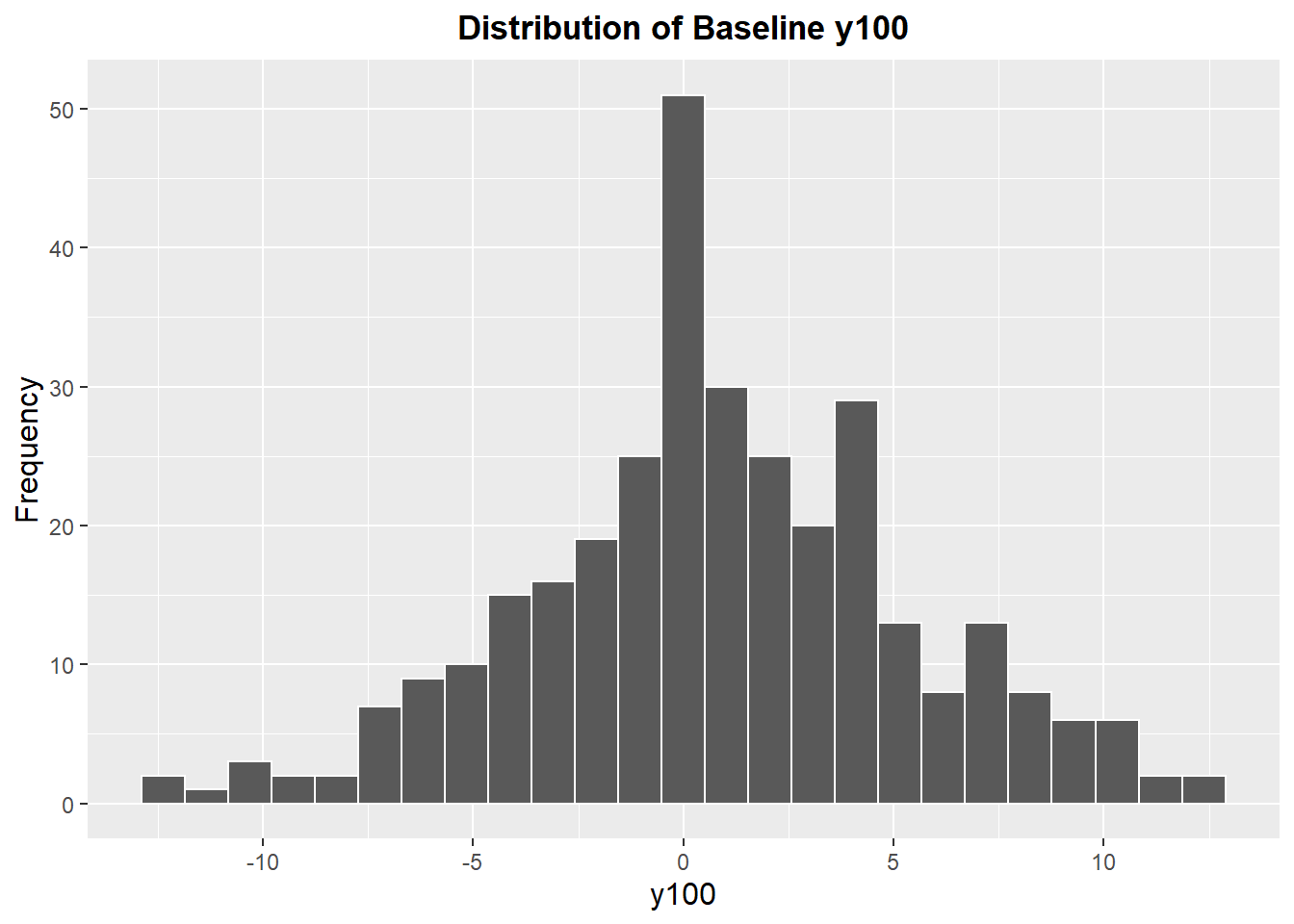
We can count that there are about 10 parts below -7.5, and about 10 parts above 10. We want to find a compromise between wanting a large enough sample to be certain that we can detect the effect of the dominant cause, and wanting to save costs. The rule of thumb given as a minimum sample size of 8 per group for a group comparison, so a sample size of 12 for each group was considered a good start (more parts could be measured or a new approach considered if the sample of 12 did not uncover a convincing pattern).
baseline.data[sort(baseline.data$y100, index.return=TRUE)$ix[1:12], c("partnum", "y100")]baseline.data[sort(baseline.data$y100, decreasing=TRUE, index.return=TRUE)$ix[1:12], c("partnum", "y100")]Analysis
groups.data <- read.delim("group-comparisons.tsv")
summary(groups.data)## daycount shift partnum y100
## Min. :1.00 Min. :1.000 Min. : 63.0 Min. :-12.2500
## 1st Qu.:1.00 1st Qu.:1.000 1st Qu.: 932.2 1st Qu.: -9.4375
## Median :1.50 Median :2.000 Median :1564.5 Median : 1.1250
## Mean :1.75 Mean :1.917 Mean :1769.2 Mean : 0.5104
## 3rd Qu.:2.25 3rd Qu.:3.000 3rd Qu.:2674.8 3rd Qu.: 10.5000
## Max. :3.00 Max. :3.000 Max. :3666.0 Max. : 12.5000
## x4 x5 x6
## Min. :0.900 Min. :-12.400 Min. :-12.400
## 1st Qu.:4.400 1st Qu.: -6.325 1st Qu.: -4.350
## Median :6.000 Median : 3.150 Median : 1.050
## Mean :5.658 Mean : 2.746 Mean : 1.642
## 3rd Qu.:7.700 3rd Qu.: 10.925 3rd Qu.: 7.950
## Max. :8.700 Max. : 17.900 Max. : 15.700The best way to get an initial impression of the data is to plot it. We can plot each of the three suspect varying inputs against the output y100 to see if a relationship exists. We can also plot the inputs against time, to try to determine the time family of variation. We know the dominant cause must act part-to-part, so if any of the inputs vary predominately over longer time scales, we can safetly rule it out. Note that from our existing process knowledge, we know the time family of x6, and we know the normal operating range of x5 and x6.
x4
ggplot(data=groups.data) + geom_point(aes(x=x4, y=y100)) +
labs(title="Plot of input x4 vs y100") +
theme(plot.title=element_text(hjust=0.5))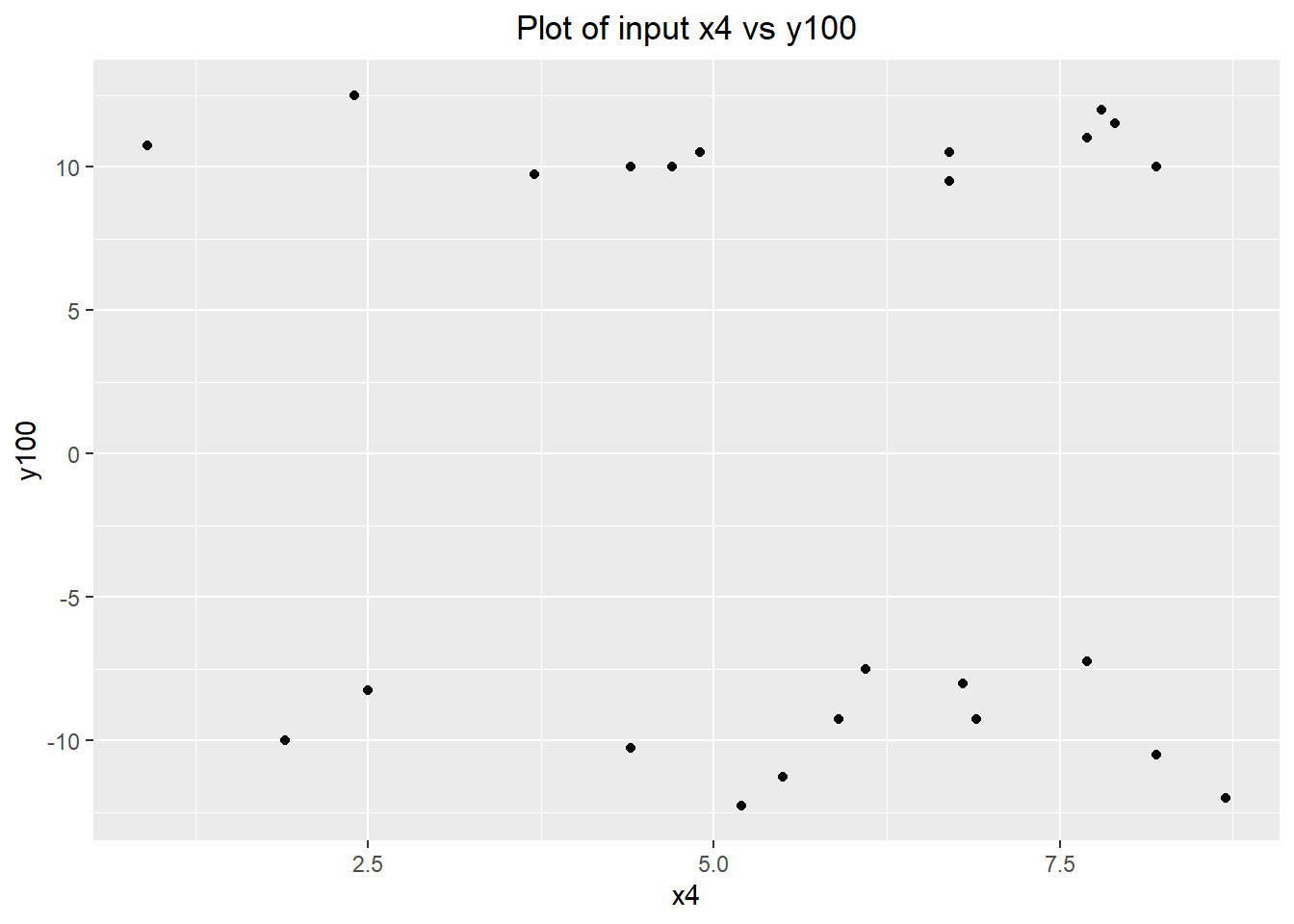
There doesn't appear to be any relationship between x4 and y100. We can confirm this quantitatively with a linear regression model:
summary(lm(y100~x4, data=groups.data))##
## Call:
## lm(formula = y100 ~ x4, data = groups.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.9296 -9.9626 0.7383 9.8758 12.2799
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.599 6.115 0.425 0.675
## x4 -0.369 1.010 -0.365 0.718
##
## Residual standard error: 10.66 on 22 degrees of freedom
## Multiple R-squared: 0.006033, Adjusted R-squared: -0.03915
## F-statistic: 0.1335 on 1 and 22 DF, p-value: 0.7183From our observations, there doesn't appear to be any significant grouping of points in time, indicating the time family is likely part-to-part (which makes sense given these are input components).
ggplot(groups.data) + geom_point(aes(x=partnum/60, y=x4)) +
labs(title="Plot of input x4 over time",
x="Hour") +
scale_x_continuous(breaks=seq(0, max(groups.data$partnum/60)+8, 8)) +
theme(plot.title=element_text(hjust=0.5))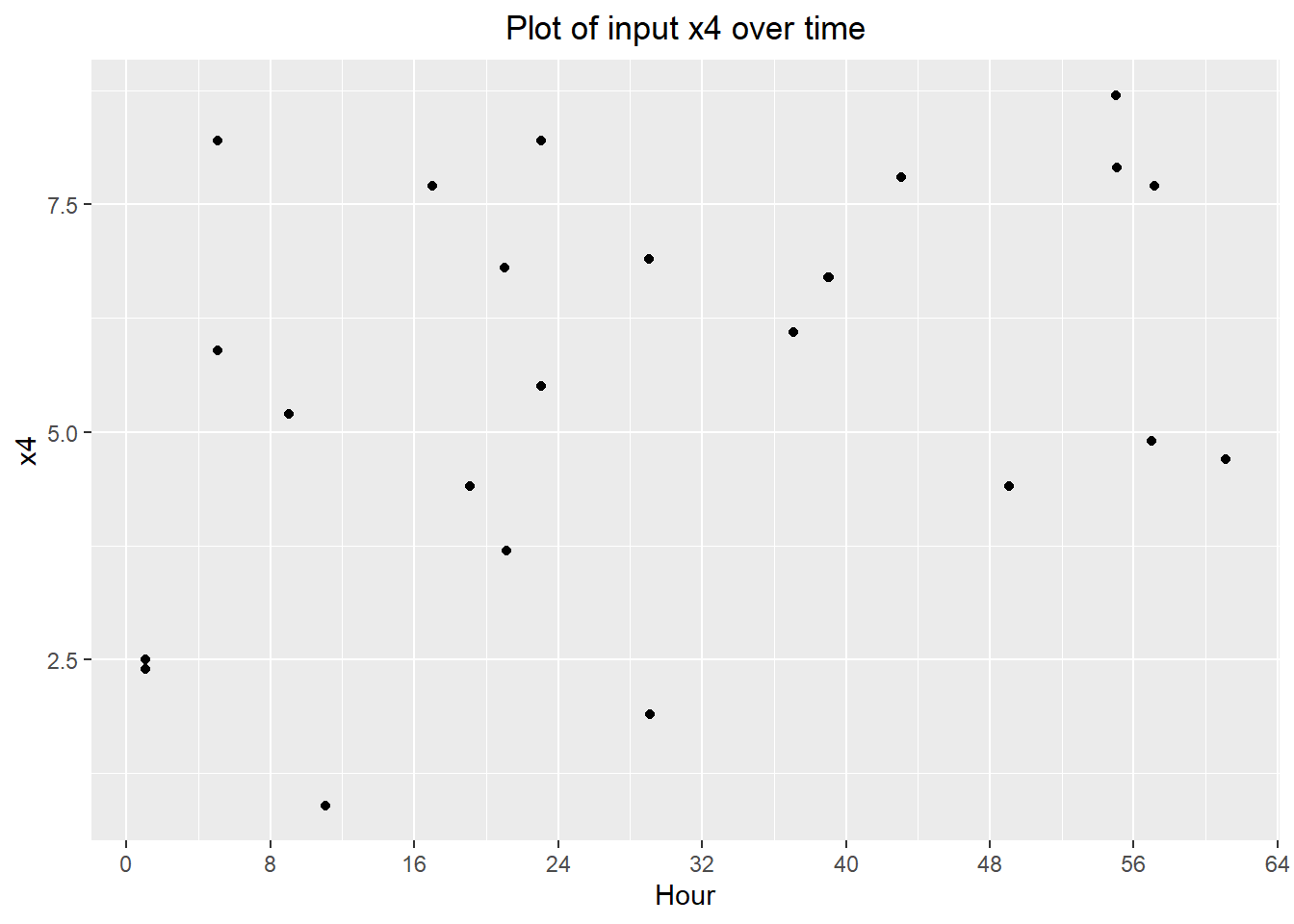
x5
ggplot(groups.data) + geom_point(aes(x=x5, y=y100)) +
geom_vline(xintercept=-17.1) +
geom_vline(xintercept=22.2) +
labs(title="Plot of input x5 vs y100") +
theme(plot.title=element_text(hjust=0.5))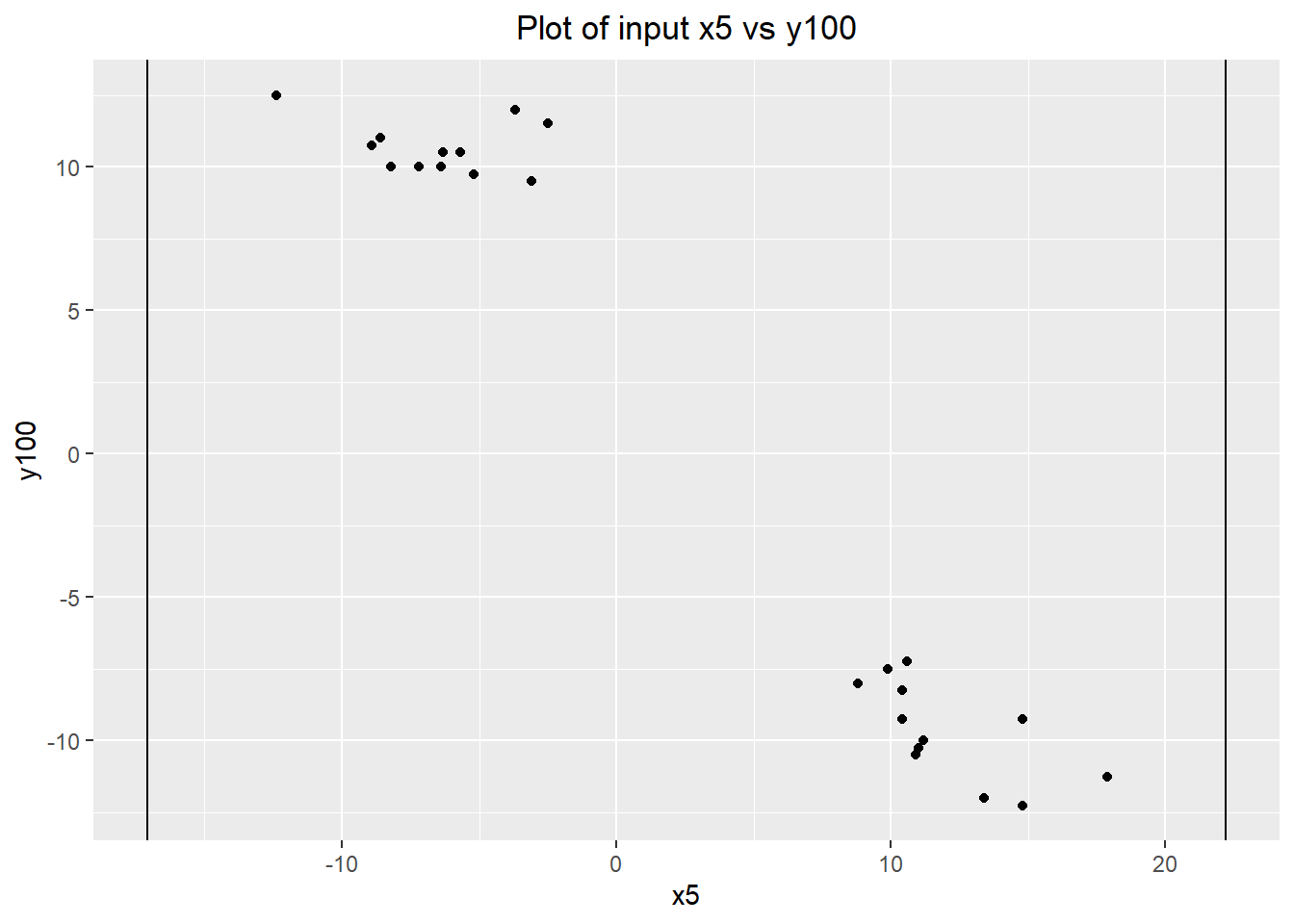
Plotting x5 against y100, a relationship is immediately obvious. The group of high parts consistently has a low value of x5 (they are all in the lower 40% of the known range of x5), while the group of low parts consistently has a high value of x5 (they are all in the upper 40% of the range of x5). The lack of middle values of x5 is also a strong indicator that x5 is the dominant cause, since the groups selected based on their value of y100. Middle values of x5 are not at all associated with extreme values of y100.
We can quantify this observation with a linear regression model. The model has an R-squared of 94.5% -- a huge amount of the variation in y100 can be explained by x5 alone. It also provides a first estimate of the relationship between x5 and y100: \[ y_{100} = -1.035 x_5 + 3.351 \]
min(groups.data[groups.data$y100 < 0, "x5"])## [1] 8.8summary(lm(y100~x5, data=groups.data))##
## Call:
## lm(formula = y100 ~ x5, data = groups.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.6815 -1.8166 -0.7047 1.0764 5.5618
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.35148 0.53075 6.315 2.35e-06 ***
## x5 -1.03468 0.05304 -19.508 2.24e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.5 on 22 degrees of freedom
## Multiple R-squared: 0.9453, Adjusted R-squared: 0.9429
## F-statistic: 380.6 on 1 and 22 DF, p-value: 2.242e-15x5 also has the expected part-to-part time family:
ggplot(groups.data) + geom_point(aes(x=partnum/60, y=x5)) +
geom_hline(yintercept=-17.1) +
geom_hline(yintercept=22.2) +
labs(title="Plot of input x5 over time",
x="Hour") +
scale_x_continuous(breaks=seq(0, max(groups.data$partnum/60)+8, 8)) +
theme(plot.title=element_text(hjust=0.5))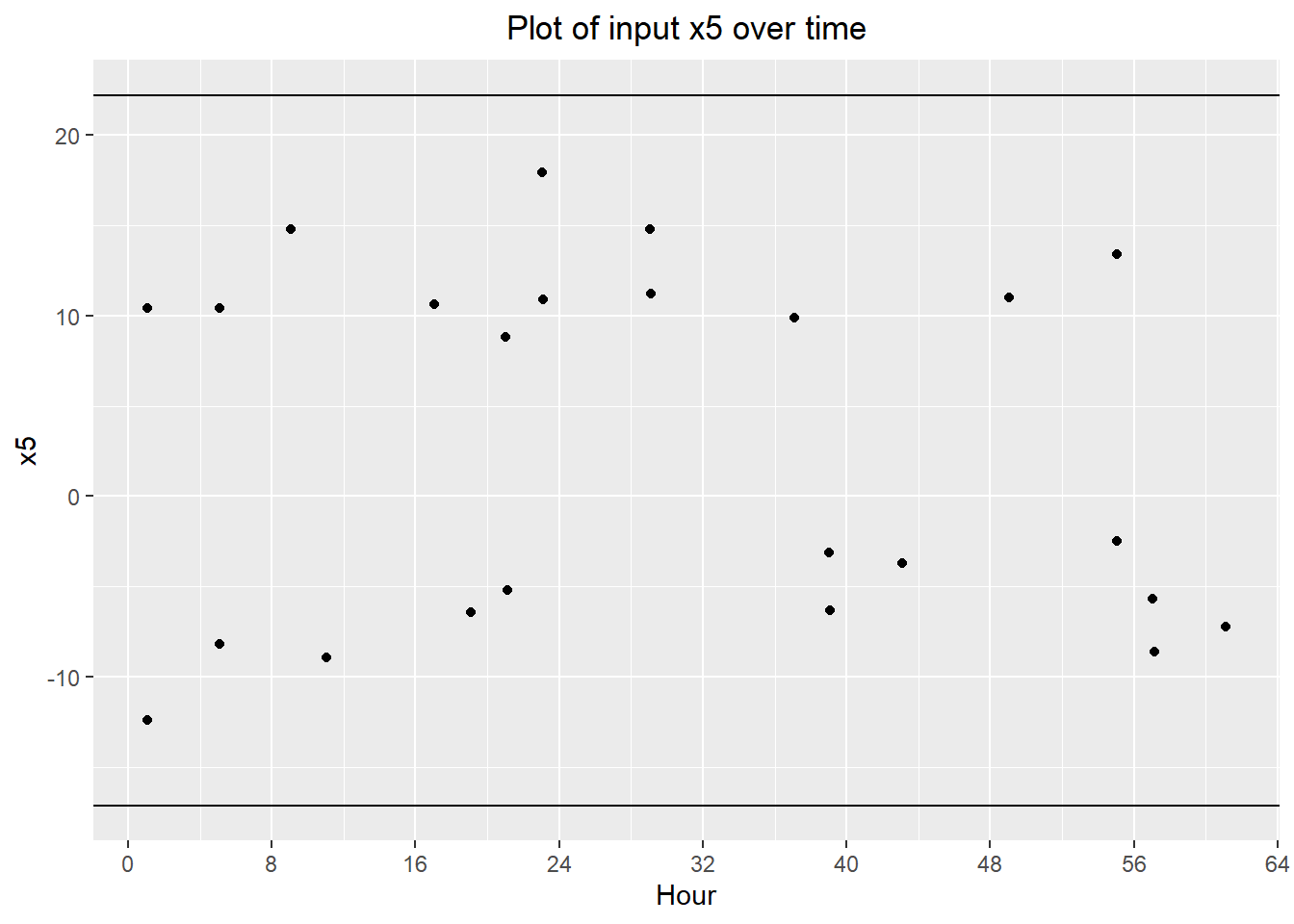
x6
We are pretty confident that we have already found our dominant cause, but we can investigate the last input for completeness. As expected, it does not have a significant relationship with y100, as illustrated by the lack of fit in a linear regression model.
ggplot(groups.data) + geom_point(aes(x=x6, y=y100)) +
geom_vline(xintercept=-14.3) +
geom_vline(xintercept=18.5) +
labs(title="Plot of input x6 vs y100") +
theme(plot.title=element_text(hjust=0.5))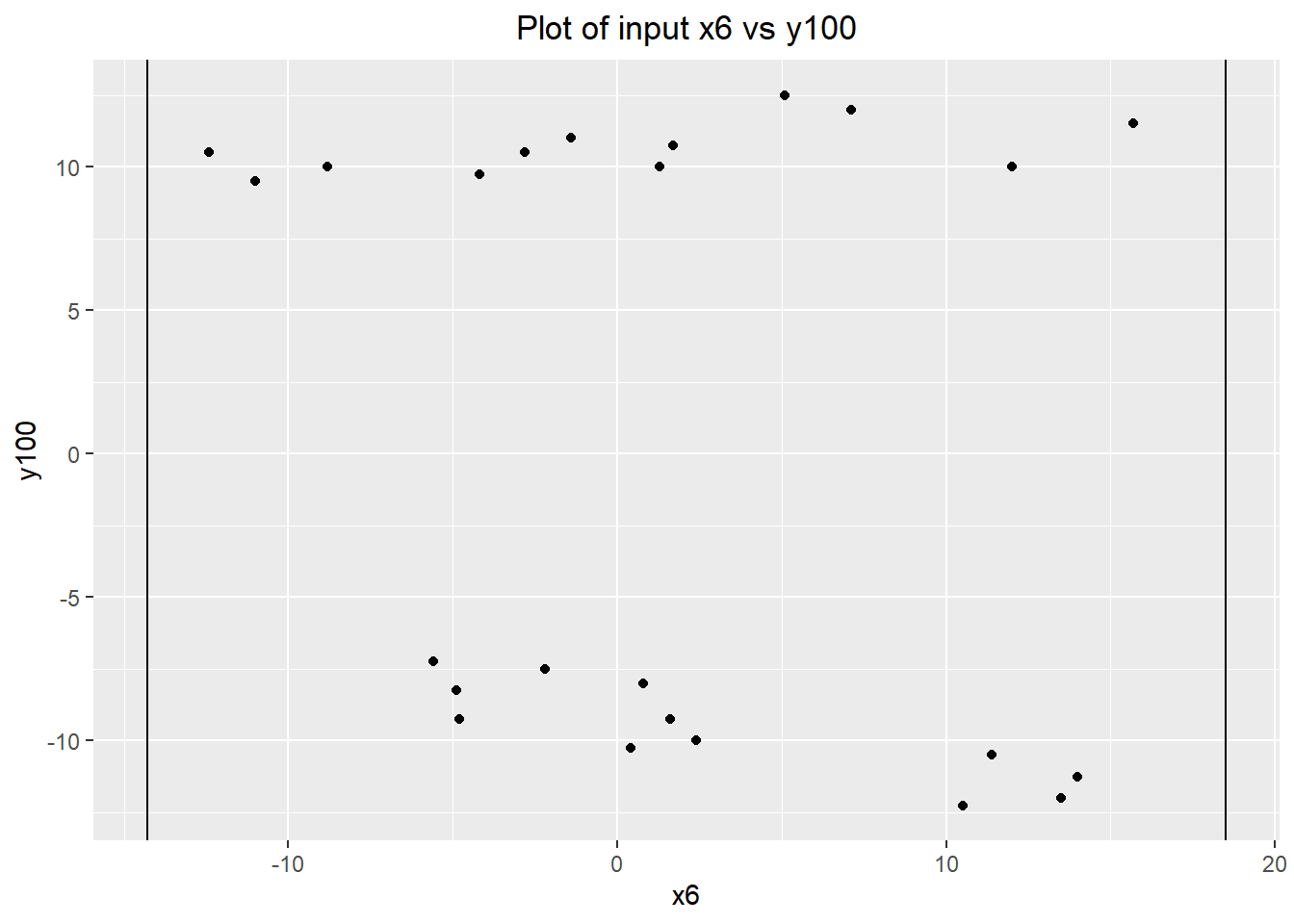
summary(lm(y100~x6, data=groups.data))##
## Call:
## lm(formula = y100 ~ x6, data = groups.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.580 -9.781 -1.418 9.452 14.961
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.9742 2.1762 0.448 0.659
## x6 -0.2825 0.2698 -1.047 0.306
##
## Residual standard error: 10.44 on 22 degrees of freedom
## Multiple R-squared: 0.04748, Adjusted R-squared: 0.004187
## F-statistic: 1.097 on 1 and 22 DF, p-value: 0.3064Conclusion
We are pretty certain that we've found our dominant cause -- the varying input x5 in component B. The next step is to experimentally verify that x5 is the dominant cause, and then we can begin the remedial journey.
Investigation 4 – Dominant Cause Verification
The purpose of this investigation is to put a cap on the diagnostic investigation of the process by experimentally verifying that x5 is the dominant cause. The experimental verification is to be absolutely sure that our observations from the previous investigation weren't caused by confounding. Given the context, this may not be strictly necessary -- it is hard to imagine a situation where some process is affecting the dimensions of the components going into the assembly, and also has a separate effect on the output. But the cost of the experiment can be kept relatively low (about $500, 5% of the original $10,000 budget), and we can use this experiment to get additional information about the process. Notably, this provides an opportunity to see the relationship between the intermediate and final output (y100 and y300) at the upper and lower extremes, and a baseline for the current values of the fixed process inputs, which we will use to improve the process in the remedial journey.
Our experiment simply fixes x5 at the maximum and minimum values in its operating range which we know from our existing process knowledge. We don't need many observations; the residual variation from the group comparison investigation was quite low, so the effect of x5 on y100 and y300 should be obvious. I chose a sample of 6 for each value of x5, with the knowledge that I could run the experiment again if the sample wasn't large enough.
verif.data <- read.delim("x5-verification.tsv")
summary(verif.data)## daycount shift partnum y100 y300
## Min. :6 Min. :2 Min. :7681 Min. :-21.7500 Min. :-22.5000
## 1st Qu.:6 1st Qu.:2 1st Qu.:7684 1st Qu.:-18.5625 1st Qu.:-16.8750
## Median :6 Median :2 Median :7686 Median : 1.3750 Median : 0.6250
## Mean :6 Mean :2 Mean :7686 Mean : 0.6875 Mean : 0.9375
## 3rd Qu.:6 3rd Qu.:2 3rd Qu.:7689 3rd Qu.: 19.3125 3rd Qu.: 19.1250
## Max. :6 Max. :2 Max. :7692 Max. : 22.2500 Max. : 23.7500
## x5
## Min. :-17.10
## 1st Qu.:-17.10
## Median : 2.55
## Mean : 2.55
## 3rd Qu.: 22.20
## Max. : 22.20Experimental Results
Right off the bat, we can conclude that x5 has a large, causal effect on both outputs. The plots below show that the effect is roughly the same for both the intermediate and final outputs.
ggplot(data=verif.data) + geom_point(aes(x=x5, y=y100)) +
labs(title="Plot of experimental x5 vs intermediate output y100") +
geom_hline(yintercept=max(baseline.data$y100), linetype="dashed") +
geom_hline(yintercept=min(baseline.data$y100), linetype="dashed") +
theme(plot.title=element_text(hjust=0.5))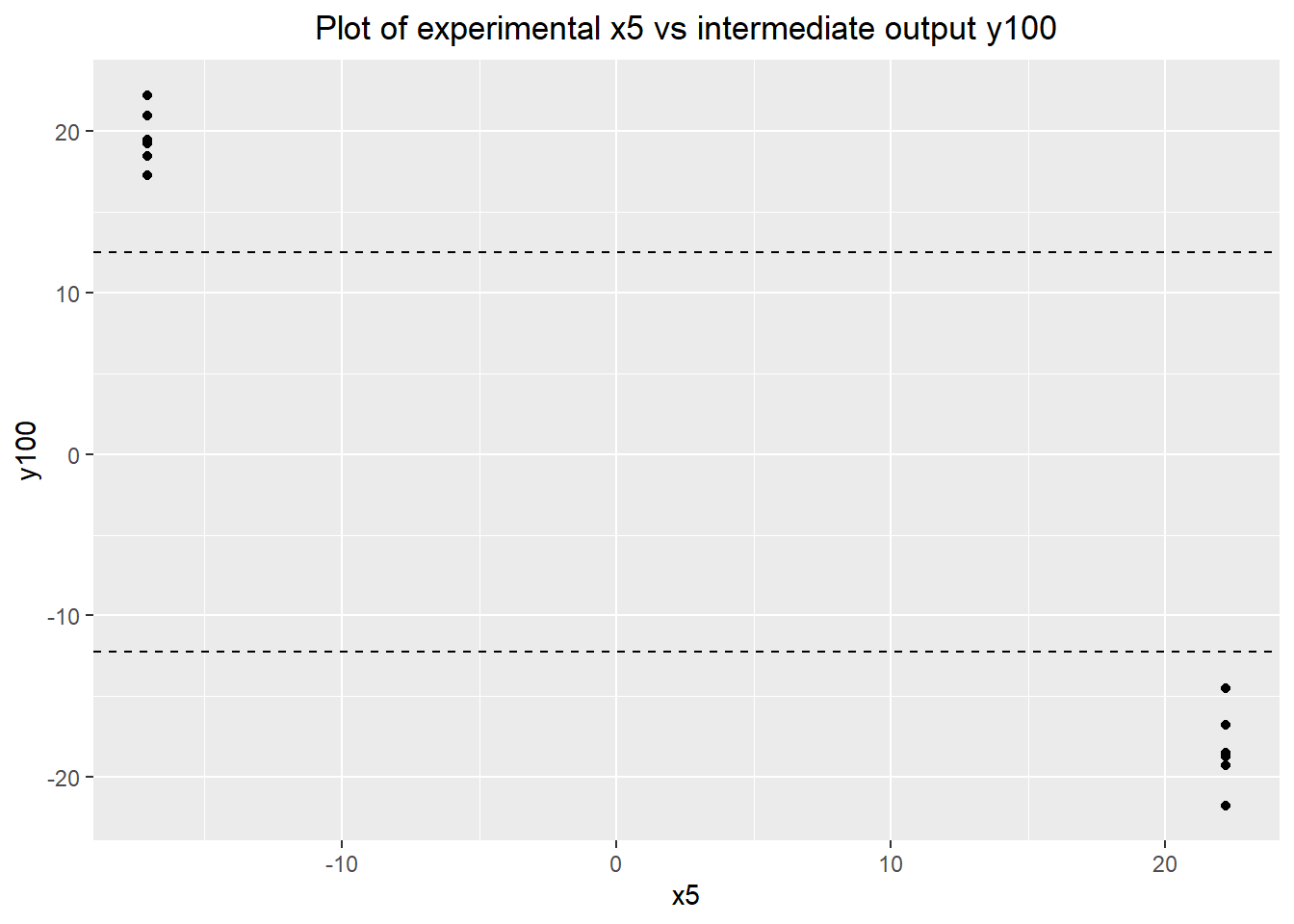
ggplot(data=verif.data) + geom_point(aes(x=x5, y=y300)) +
labs(title="Plot of experimental x5 vs final output y300") +
geom_hline(yintercept=12.5, linetype="dashed") +
geom_hline(yintercept=-12.5, linetype="dashed") +
theme(plot.title=element_text(hjust=0.5))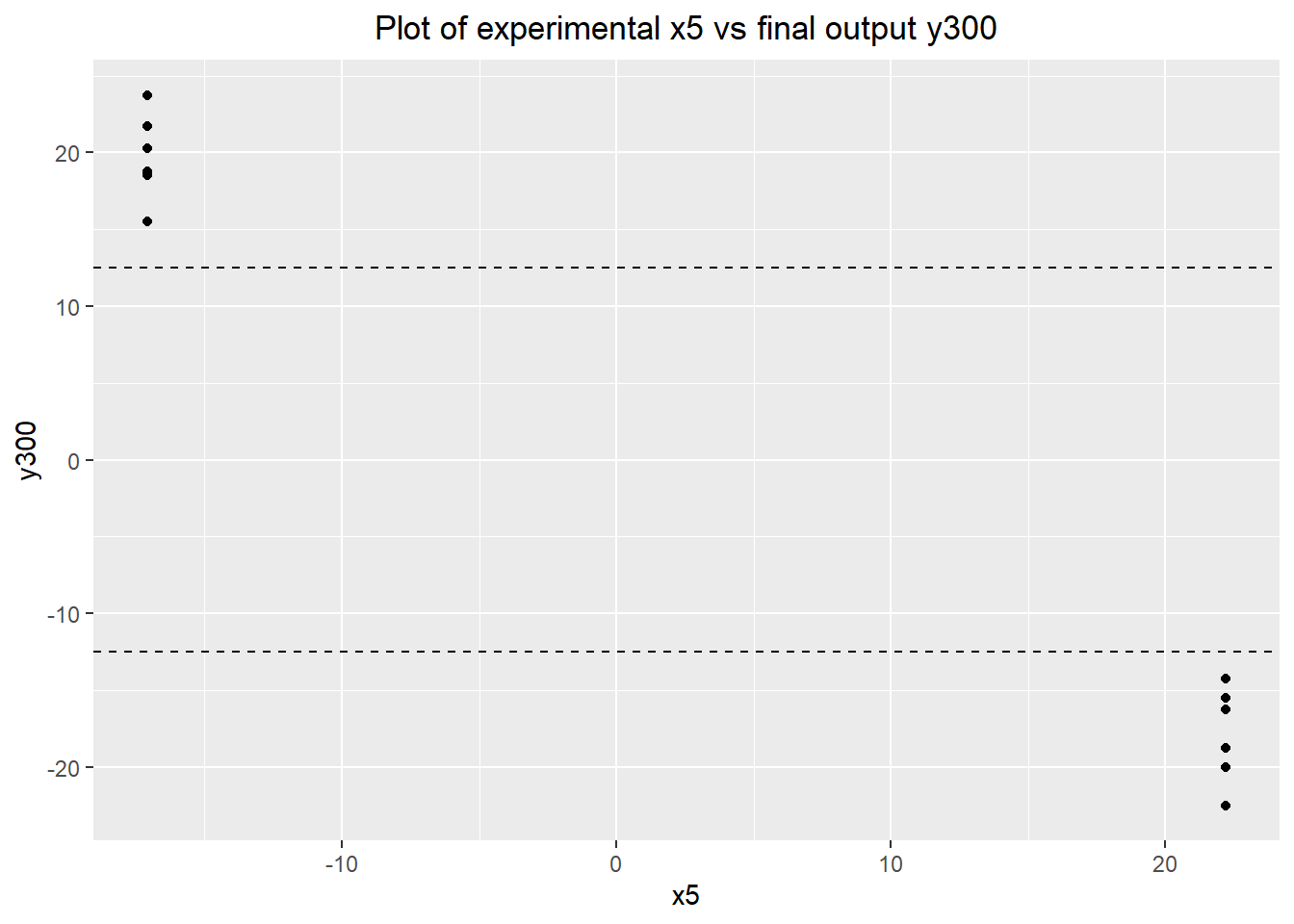
We can also get an estimate of the relationship between y100 and y300 at these very extreme values, and verify that the relationship is linear with a coefficient of about 1. This was not observed previously in the data (in the simulation, we arrived in the process early and missed the variation transmission investigation, and do not have access to those results), so it will play a part in our future conclusions drawn from the behaviour of y100.
ggplot(data=verif.data) + geom_point(aes(x=y100, y=y300)) +
labs(title="Plot of y100 vs y300") +
stat_smooth(aes(x=y100, y=y300), method="lm")## `geom_smooth()` using formula 'y ~ x'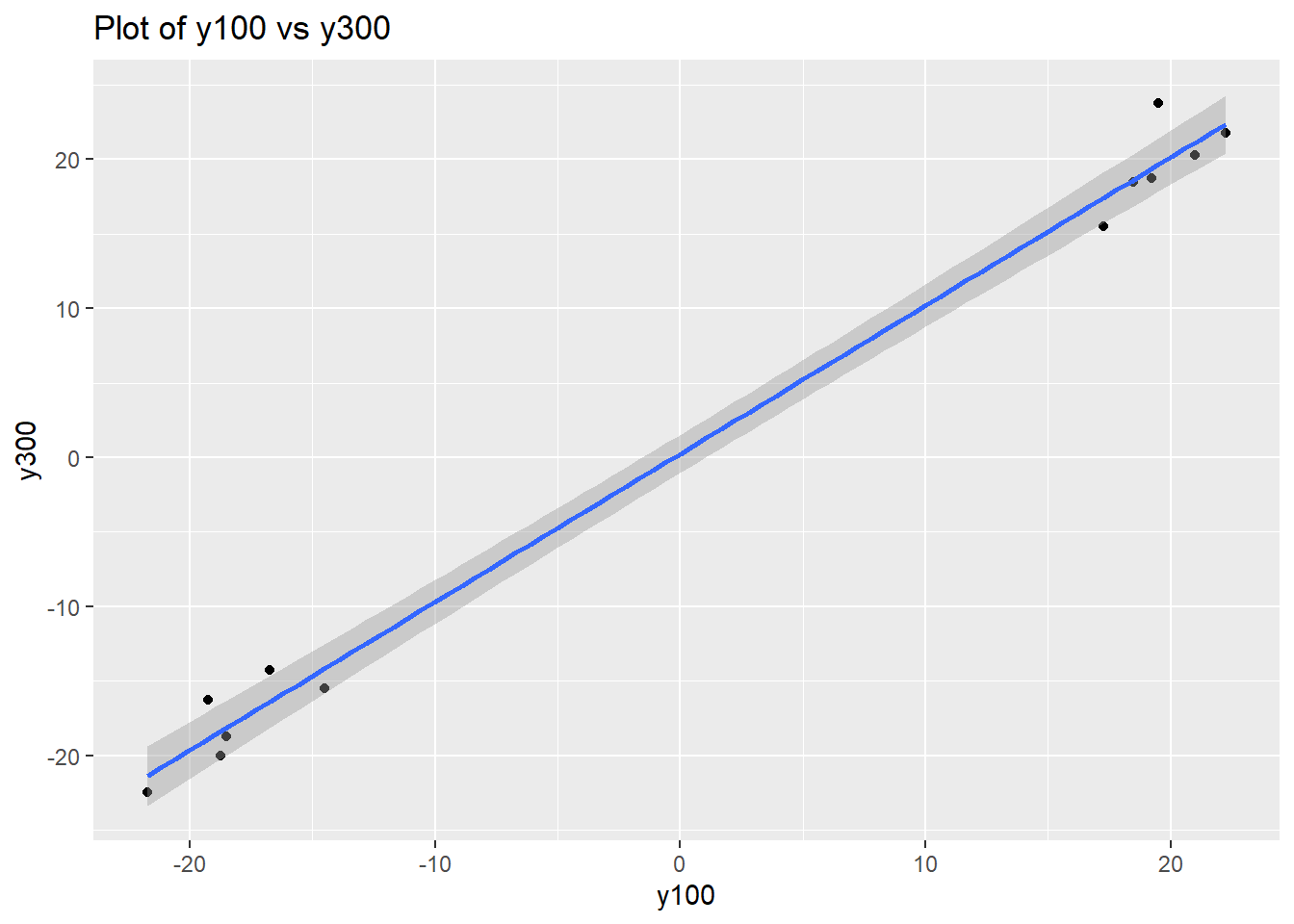
y300.y100.model <- lm(y300 ~ y100, data=verif.data)
summary(y300.y100.model)##
## Call:
## lm(formula = y300 ~ y100, data = verif.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.8986 -1.1888 -0.6272 0.4301 4.1152
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.25421 0.57564 0.442 0.668
## y100 0.99388 0.03022 32.891 1.59e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.993 on 10 degrees of freedom
## Multiple R-squared: 0.9908, Adjusted R-squared: 0.9899
## F-statistic: 1082 on 1 and 10 DF, p-value: 1.592e-11Going by the observational group comparison investigation and this verification experiment, a linear model for the relationship between x5 and the outputs seems appropriate. We can quantify the relationship with a linear regression model:
y300.x5.model <- lm(y300 ~ x5, data=verif.data)
summary(y300.x5.model)##
## Call:
## lm(formula = y300 ~ x5, data = verif.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.6250 -1.4688 -0.1875 2.0938 4.0000
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.37882 0.86827 3.891 0.003 **
## x5 -0.95738 0.04382 -21.848 9.03e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.983 on 10 degrees of freedom
## Multiple R-squared: 0.9795, Adjusted R-squared: 0.9774
## F-statistic: 477.3 on 1 and 10 DF, p-value: 9.029e-10y100.x5.model <- lm(y100 ~ x5, data=verif.data)
summary(y100.x5.model)##
## Call:
## lm(formula = y100 ~ x5, data = verif.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.5000 -1.0313 -0.3125 1.4063 3.7500
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.14504 0.62242 5.053 0.000497 ***
## x5 -0.96374 0.03141 -30.681 3.17e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.138 on 10 degrees of freedom
## Multiple R-squared: 0.9895, Adjusted R-squared: 0.9884
## F-statistic: 941.3 on 1 and 10 DF, p-value: 3.173e-11Investigation 5 – Desensitizer
Having established the dominant cause of process variation, we are into the remedial journey where we investigate solutions to the problem of excess variation. There are several options available to us which can reduce process variation, of which 4 involve manipulating process inputs which are normally fixed. There are two flavours of this: active control, and desensitization/robustness. With active control, we use an input "adjuster" which can reliably change the centre of the process. With desensitization/robustness, we use an input which reduces the effect of the dominant cause.
The most effective way for us to explore desensitization is to experimentally fix upper and lower values of the dominant cause and test out different combinations of the inputs. By doing this first, we also get information on the adjuster potential of each input, which could save us hundreds of dollars in investigation costs. After this initial exploration, we'll do a more in-depth investigation of the most promising desensitizer and adjuster to properly quantify their effect.
Focusing on the preassembly step, we have 6 inputs which can be changed. 4 of these are continuous inputs, and 2 of them are categorical. The categorical inputs are the least expensive to change, so I used them as my first focus. The two, z5 and z6, have 2 and 4 levels respectively, so it was inexpensive to run a full factorial experiment (each level of z5, z6, and the dominant cause x5). We can make use of the fact that we've been running all of our previous investigations with z5 and z6 at their default values and in particular use the results of the verification experiment.
desen.cat.df <- read.delim("desensitizer-z5-z6.tsv")
summary(desen.cat.df)## daycount shift partnum y100 z5
## Min. :6 Min. :3 Min. :8161 Min. :-17.250 Min. :1.000
## 1st Qu.:6 1st Qu.:3 1st Qu.:8164 1st Qu.: 7.062 1st Qu.:1.000
## Median :6 Median :3 Median :8168 Median : 21.750 Median :2.000
## Mean :6 Mean :3 Mean :8168 Mean : 22.018 Mean :1.571
## 3rd Qu.:6 3rd Qu.:3 3rd Qu.:8171 3rd Qu.: 37.625 3rd Qu.:2.000
## Max. :6 Max. :3 Max. :8174 Max. : 67.000 Max. :2.000
## z6 x5
## Min. :1.000 Min. :-17.10
## 1st Qu.:2.000 1st Qu.:-17.10
## Median :3.000 Median : 2.55
## Mean :2.714 Mean : 2.55
## 3rd Qu.:3.750 3rd Qu.: 22.20
## Max. :4.000 Max. : 22.20verif.data$z5 <- 1
verif.data$z6 <- 1
desen.cat.df$y300 <- NA
desen.cat.full <- rbind(desen.cat.df, verif.data)
summary(desen.cat.full)## daycount shift partnum y100 z5
## Min. :6 Min. :2.000 Min. :7681 Min. :-21.75 Min. :1.000
## 1st Qu.:6 1st Qu.:2.000 1st Qu.:7687 1st Qu.:-12.81 1st Qu.:1.000
## Median :6 Median :3.000 Median :8162 Median : 16.38 Median :1.000
## Mean :6 Mean :2.538 Mean :7946 Mean : 12.17 Mean :1.308
## 3rd Qu.:6 3rd Qu.:3.000 3rd Qu.:8168 3rd Qu.: 26.56 3rd Qu.:2.000
## Max. :6 Max. :3.000 Max. :8174 Max. : 67.00 Max. :2.000
##
## z6 x5 y300
## Min. :1.000 Min. :-17.10 Min. :-22.5000
## 1st Qu.:1.000 1st Qu.:-17.10 1st Qu.:-16.8750
## Median :1.000 Median : 2.55 Median : 0.6250
## Mean :1.923 Mean : 2.55 Mean : 0.9375
## 3rd Qu.:3.000 3rd Qu.: 22.20 3rd Qu.: 19.1250
## Max. :4.000 Max. : 22.20 Max. : 23.7500
## NA's :14Analysis
agg.z6 <- data.frame(z6=rep(1:4, 2),
y100=c(tapply(desen.cat.full[desen.cat.full$x5 == -17.10, "y100"],
desen.cat.full[desen.cat.full$x5 == -17.10, "z6"],
mean),
tapply(desen.cat.full[desen.cat.full$x5 == 22.2, "y100"],
desen.cat.full[desen.cat.full$x5 == 22.2, "z6"],
mean)),
x5=c(rep(-17.10, 4), rep(22.2, 4))
)
ggplot(data=desen.cat.full) + geom_point(aes(x=z6, y=y100,
color=as.factor(x5),
shape=as.factor(z5)),
position=position_jitter(0.02)) +
geom_line(aes(x=z6, y=y100, color=as.factor(x5)), data=agg.z6) +
labs(title="Plot of experiment with fixed input z6") +
scale_x_continuous(breaks=c(1, 2, 3, 4), minor_breaks=NULL) +
scale_color_discrete(name="x5") +
scale_shape_discrete(name="z5") +
theme(plot.title=element_text(hjust=0.5))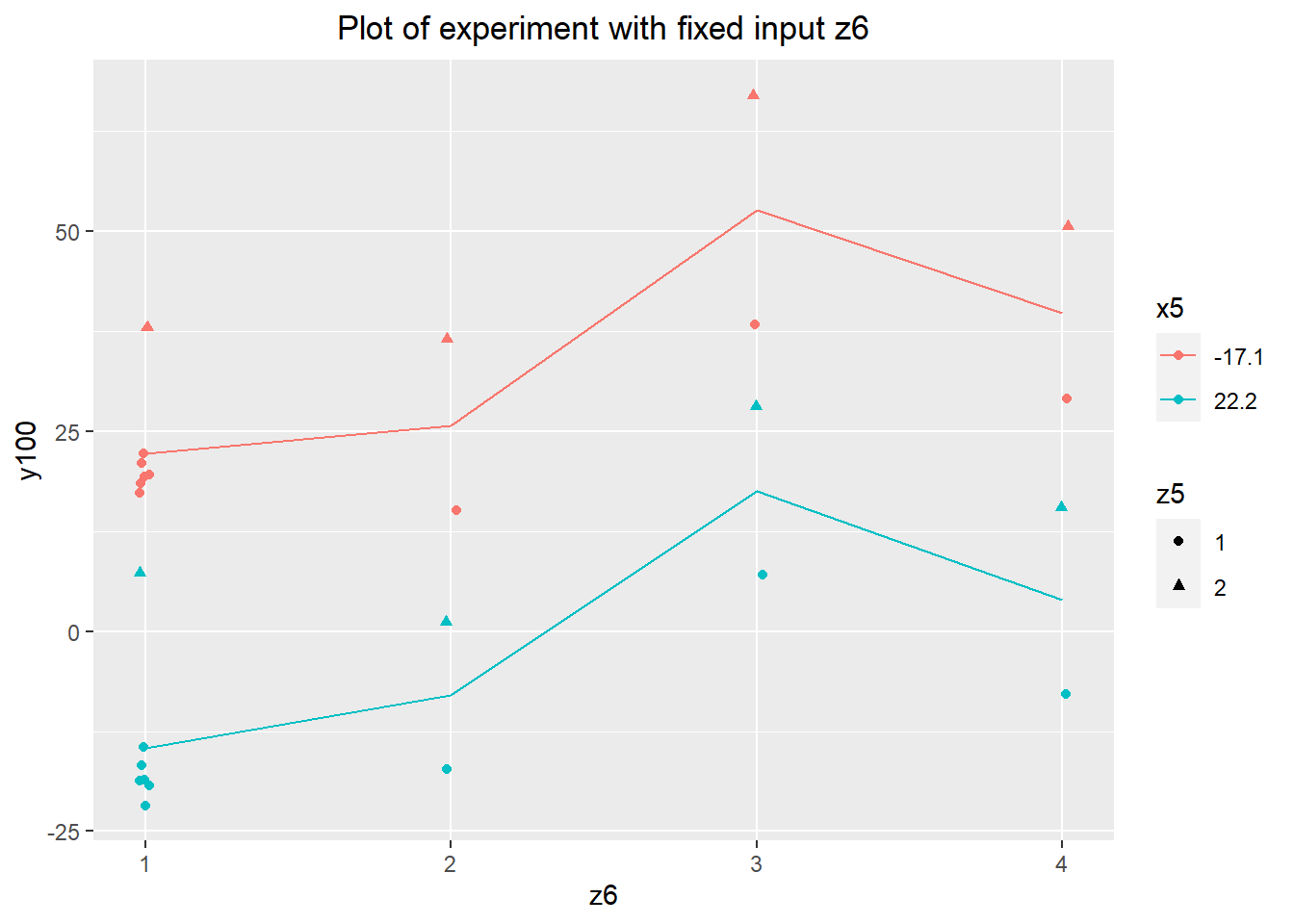
The desensitizer will result in values of y100 being closer or further apart at the extreme levels of x5. This would show up in the plot above as a difference in slopes of the red and pink lines corresponding to the average values of y100 at each level of the input, for the low and high values of x5 respectively. That effect isn't visible here, which can be verified by an ANOVA (a desensitizer would show up as a significant interaction term between the input and x5).
anova(lm(y100~as.factor(z6)*x5 + as.factor(z5)*x5, data=desen.cat.full))The ANOVA indicates that there's no interaction between z5 and x5 either. The plot of the data tells the same story. The levels of the input appear to have a significant effect on the average level of y100, but these inputs are categorical and so would not make good adjusters. We can safely ignore these categorical inputs going forward.
agg.z5 <- data.frame(z5=rep(1:2, 2),
y100=c(tapply(desen.cat.full[desen.cat.full$x5 == -17.10, "y100"],
desen.cat.full[desen.cat.full$x5 == -17.10, "z5"],
mean),
tapply(desen.cat.full[desen.cat.full$x5 == 22.2, "y100"],
desen.cat.full[desen.cat.full$x5 == 22.2, "z5"],
mean)),
x5=c(rep(-17.10, 2), rep(22.2, 2))
)
ggplot(data=desen.cat.full) + geom_point(aes(x=z5, y=y100,
color=as.factor(x5),
shape=as.factor(z6)),
position=position_jitter(0.02)) +
geom_line(aes(x=z5, y=y100, color=as.factor(x5)), data=agg.z5) +
labs(title="Plot of experiment with fixed input z5") +
scale_x_continuous(breaks=c(1, 2), minor_breaks=NULL) +
scale_color_discrete(name="x5") +
scale_shape_discrete(name="z6") +
theme(plot.title=element_text(hjust=0.5))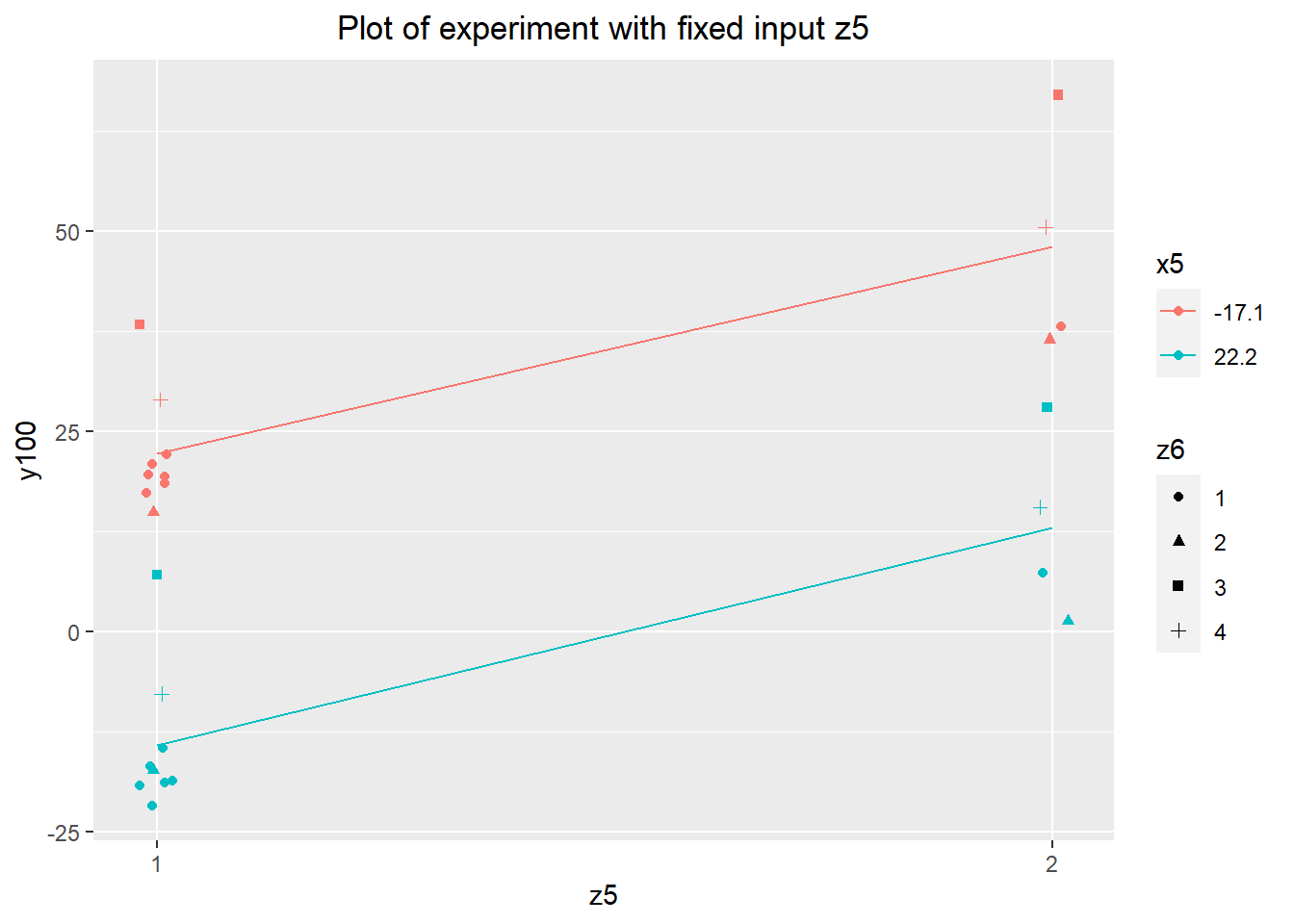
Having looked at the least expensive fixed inputs to implement as a desensitizer, we have 4 candidates inputs left, all continuous. Changing the levels of these inputs is somewhat expensive, making an experiment with all 4 at once infeasible (a fractional factorial experiment has the same problem). This isn't a huge deal, since we don't particularly care about interactions between the fixed inputs at the moment. Instead, we'll start by looking at the two least expensive inputs to use: z1 and z4. I ran another full factorial experiment, this time using the two extreme values of each variable.
desen.z1.z4 <- read.delim("desensitizer-z1-z4.tsv")
summary(desen.z1.z4)## daycount shift partnum y100 z1
## Min. :7 Min. :1 Min. :8641 Min. :-35.0000 Min. :68
## 1st Qu.:7 1st Qu.:1 1st Qu.:8643 1st Qu.:-21.5625 1st Qu.:68
## Median :7 Median :1 Median :8644 Median : 1.1250 Median :81
## Mean :7 Mean :1 Mean :8644 Mean : 0.3438 Mean :81
## 3rd Qu.:7 3rd Qu.:1 3rd Qu.:8646 3rd Qu.: 16.4375 3rd Qu.:94
## Max. :7 Max. :1 Max. :8648 Max. : 51.0000 Max. :94
## z4 x5
## Min. :62 Min. :-17.10
## 1st Qu.:62 1st Qu.:-17.10
## Median :67 Median : 2.55
## Mean :67 Mean : 2.55
## 3rd Qu.:72 3rd Qu.: 22.20
## Max. :72 Max. : 22.20agg.z1 <- data.frame(z1=rep(c(68, 94), 2),
y100=c(tapply(desen.z1.z4[desen.z1.z4$x5 == -17.10, "y100"],
desen.z1.z4[desen.z1.z4$x5 == -17.10, "z1"],
mean),
tapply(desen.z1.z4[desen.z1.z4$x5 == 22.2, "y100"],
desen.z1.z4[desen.z1.z4$x5 == 22.2, "z1"],
mean)),
x5=c(rep(-17.10, 2), rep(22.2, 2))
)
verif.data$z1 <- 81
verif.data$z4 <- 67
verif.data[,c("y100", "z1", "z4")]z1.z4.agg <- rbind(desen.z1.z4[,c("y100", "z1", "z4", "x5")],
verif.data[,c("y100", "z1", "z4", "x5")])
ggplot(data=z1.z4.agg) + geom_point(aes(x=z1, y=y100,
color=as.factor(x5),
shape=as.factor(z4))) +
geom_line(aes(x=z1, y=y100, color=as.factor(x5)), data=agg.z1) +
labs(title="Plot of experiment with fixed input z1") +
scale_x_continuous(breaks=seq(68, 94, length.out=3)) +
scale_color_discrete(name="x5") +
scale_shape_discrete(name="z4") +
theme(plot.title=element_text(hjust=0.5))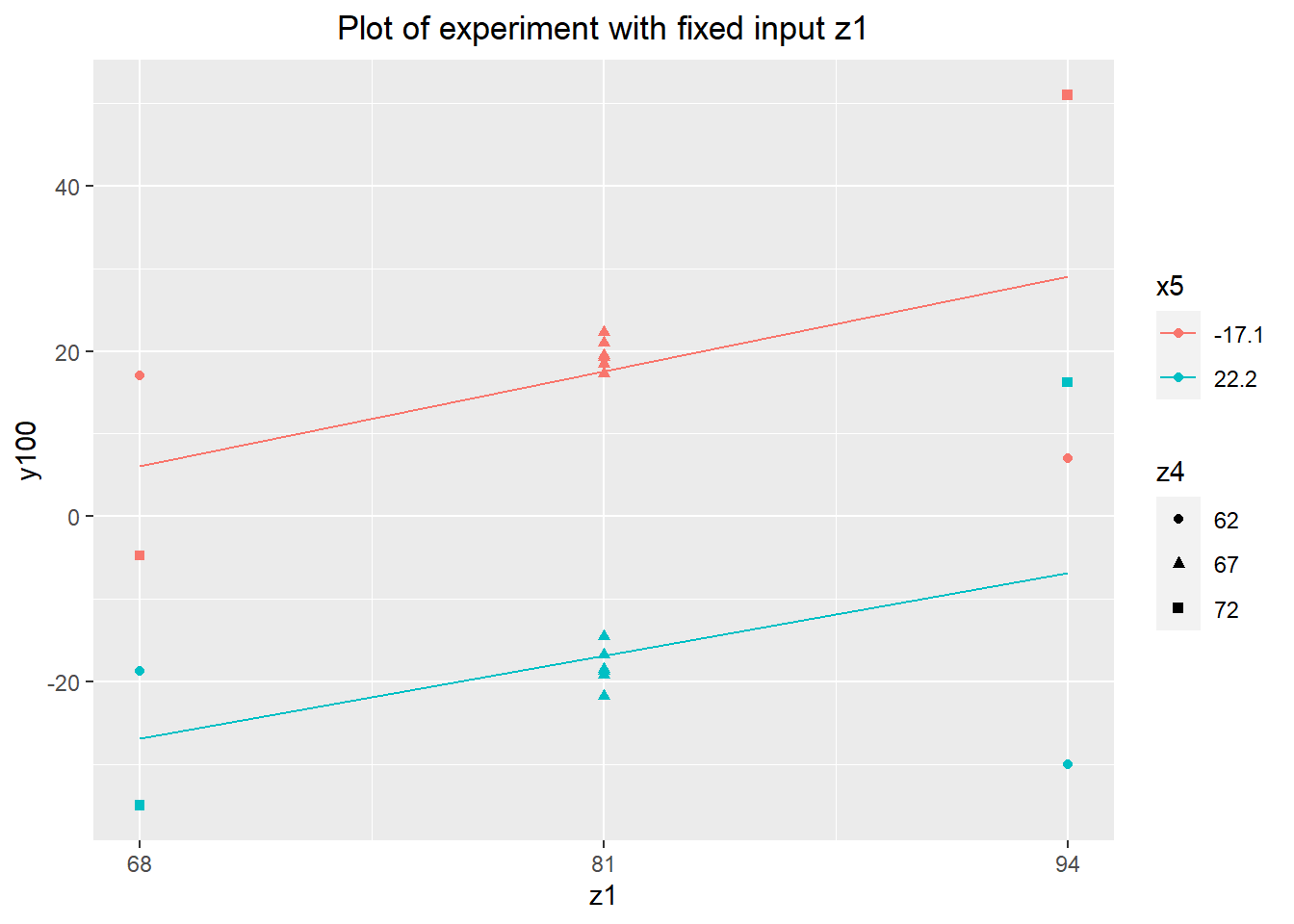
agg.z4 <- data.frame(z4=rep(c(62, 72), 2),
y100=c(tapply(desen.z1.z4[desen.z1.z4$x5 == -17.10, "y100"],
desen.z1.z4[desen.z1.z4$x5 == -17.10, "z4"],
mean),
tapply(desen.z1.z4[desen.z1.z4$x5 == 22.2, "y100"],
desen.z1.z4[desen.z1.z4$x5 == 22.2, "z4"],
mean)),
x5=c(rep(-17.10, 2), rep(22.2, 2))
)
ggplot(data=z1.z4.agg) + geom_point(aes(x=z4, y=y100,
color=as.factor(x5),
shape=as.factor(z1))) +
geom_line(aes(x=z4, y=y100, color=as.factor(x5)), data=agg.z4) +
labs(title="Plot of experiment with fixed input z4") +
scale_x_continuous(breaks=seq(62, 72, length.out=3)) +
scale_color_discrete(name="x5") +
scale_shape_discrete(name="z1") +
theme(plot.title=element_text(hjust=0.5))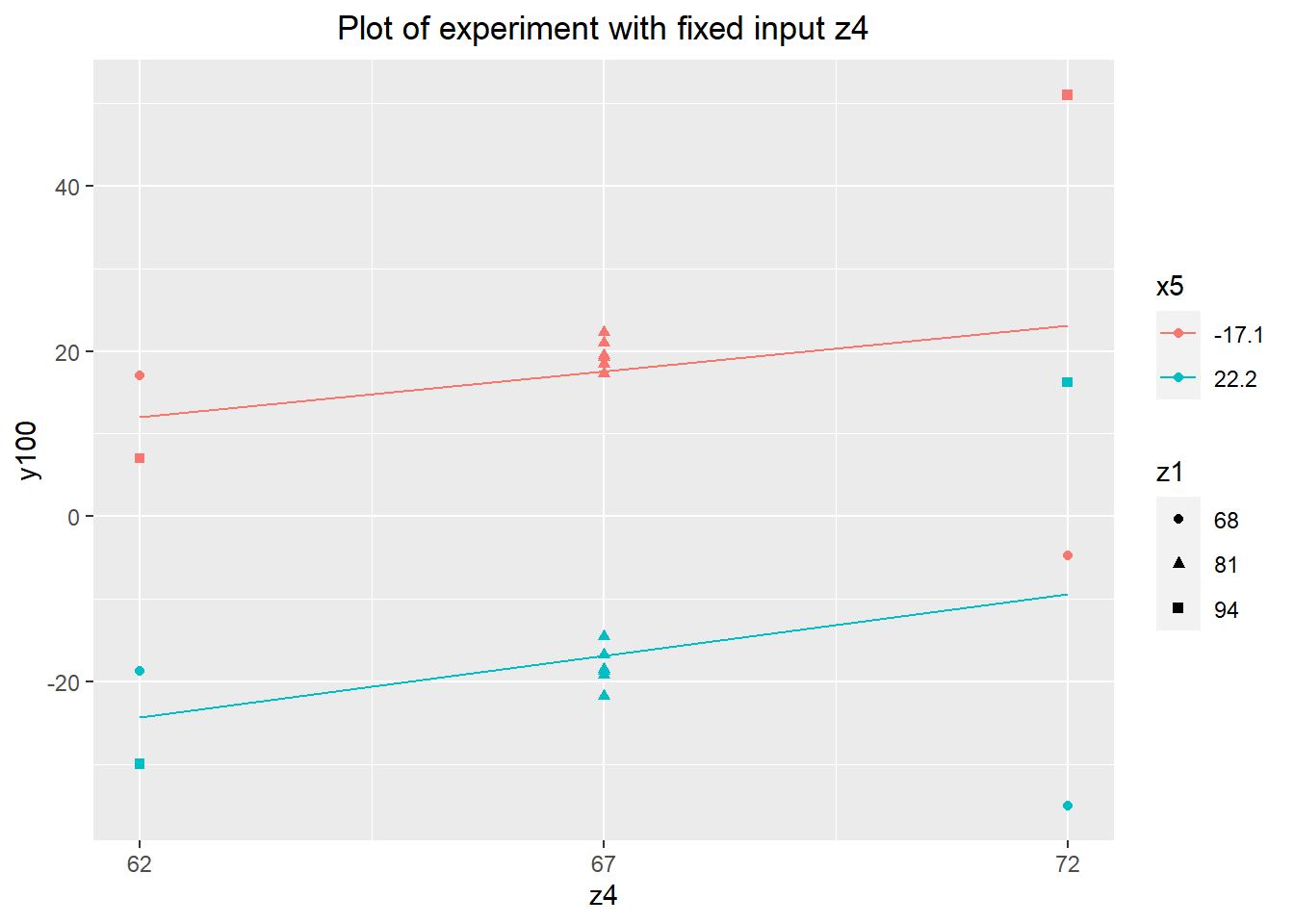
Again, there's no obvious desensitizer effect. However, both inputs appear to change the process center, with z1 changing y100 by around \(\pm 10\) over its range. This makes z1 a very promising candidate for use as an adjuster.
Without any positive results from the less expensive of the continuous fixed inputs, a final set of experiments was run using z2 and z3. Looking at these last two inputs, we have our best candidate desensitizer: z3. The extreme upper values of z3 reduce the range of y100 to about \(\pm 12.5\), a reduction of about 66% from about \(\pm 19\) in the verification experiment. This isn't as strong a reduction as we might have hoped, but it's worth exploring further and considering for the final variation reduction approach.
desen.z2.z3 <- read.delim("desensitizer-z2-z3.tsv")
summary(desen.z2.z3)## daycount shift partnum y100 z2
## Min. :7 Min. :2 Min. :9121 Min. :-35.5000 Min. :24
## 1st Qu.:7 1st Qu.:2 1st Qu.:9123 1st Qu.:-17.8125 1st Qu.:24
## Median :7 Median :2 Median :9124 Median : -2.0000 Median :31
## Mean :7 Mean :2 Mean :9124 Mean : 0.3438 Mean :31
## 3rd Qu.:7 3rd Qu.:2 3rd Qu.:9126 3rd Qu.: 20.4375 3rd Qu.:38
## Max. :7 Max. :2 Max. :9128 Max. : 36.7500 Max. :38
## z3 x5
## Min. : 6 Min. :-17.10
## 1st Qu.: 6 1st Qu.:-17.10
## Median :19 Median : 2.55
## Mean :19 Mean : 2.55
## 3rd Qu.:32 3rd Qu.: 22.20
## Max. :32 Max. : 22.20agg.z2 <- data.frame(z2=rep(c(24, 38), 2),
y100=c(tapply(desen.z2.z3[desen.z2.z3$x5 == -17.10, "y100"],
desen.z2.z3[desen.z2.z3$x5 == -17.10, "z2"],
mean),
tapply(desen.z2.z3[desen.z2.z3$x5 == 22.2, "y100"],
desen.z2.z3[desen.z2.z3$x5 == 22.2, "z2"],
mean)),
x5=c(rep(-17.10, 2), rep(22.2, 2))
)
verif.data$z2 <- 31
verif.data$z3 <- 19
z2.z3.agg <- rbind(desen.z2.z3[,c("y100", "z2", "z3", "x5")],
verif.data[,c("y100", "z2", "z3", "x5")])
ggplot(data=z2.z3.agg) + geom_point(aes(x=z2, y=y100,
color=as.factor(x5),
shape=as.factor(z3))) +
geom_line(aes(x=z2, y=y100, color=as.factor(x5)), data=agg.z2) +
labs(title="Plot of experiment with fixed input z2") +
scale_x_continuous(breaks=seq(24, 38, length.out=3)) +
scale_color_discrete(name="x5") +
scale_shape_discrete(name="z3") +
theme(plot.title=element_text(hjust=0.5))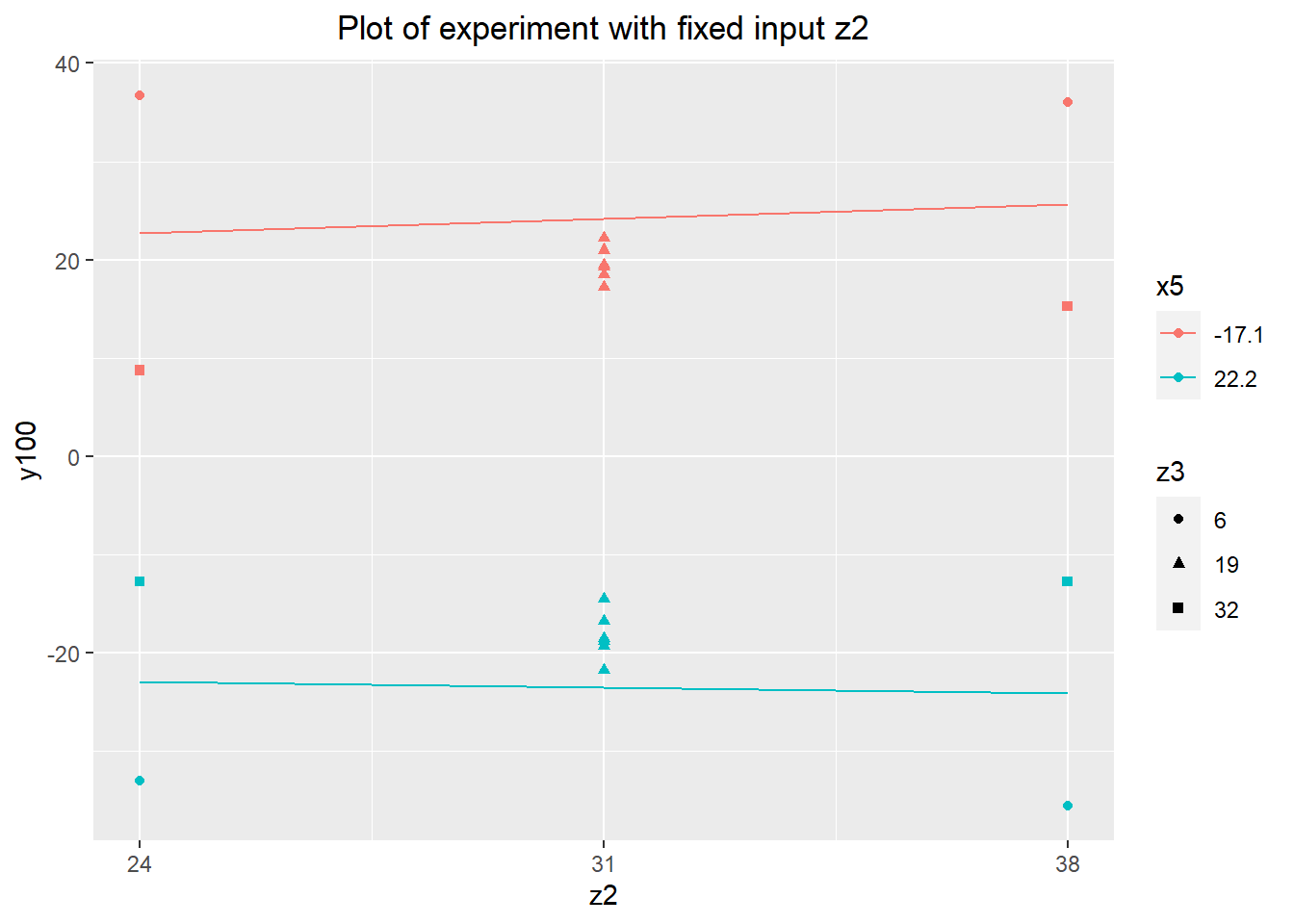
agg.z3 <- data.frame(z3=rep(c(6, 32), 2),
y100=c(tapply(desen.z2.z3[desen.z2.z3$x5 == -17.10, "y100"],
desen.z2.z3[desen.z2.z3$x5 == -17.10, "z3"],
mean),
tapply(desen.z2.z3[desen.z2.z3$x5 == 22.2, "y100"],
desen.z2.z3[desen.z2.z3$x5 == 22.2, "z3"],
mean)),
x5=c(rep(-17.10, 2), rep(22.2, 2))
)
agg.z3ggplot(data=z2.z3.agg) + geom_point(aes(x=z3, y=y100,
color=as.factor(x5),
shape=as.factor(z2)),
position=position_dodge(1)) +
geom_line(aes(x=z3, y=y100, color=as.factor(x5)), data=agg.z3) +
labs(title="Plot of experiment results with fixed input z3") +
scale_x_continuous(breaks=seq(6, 32, length.out=3)) +
scale_color_discrete(name="x5") +
scale_shape_discrete(name="z2") +
theme(plot.title=element_text(hjust=0.5))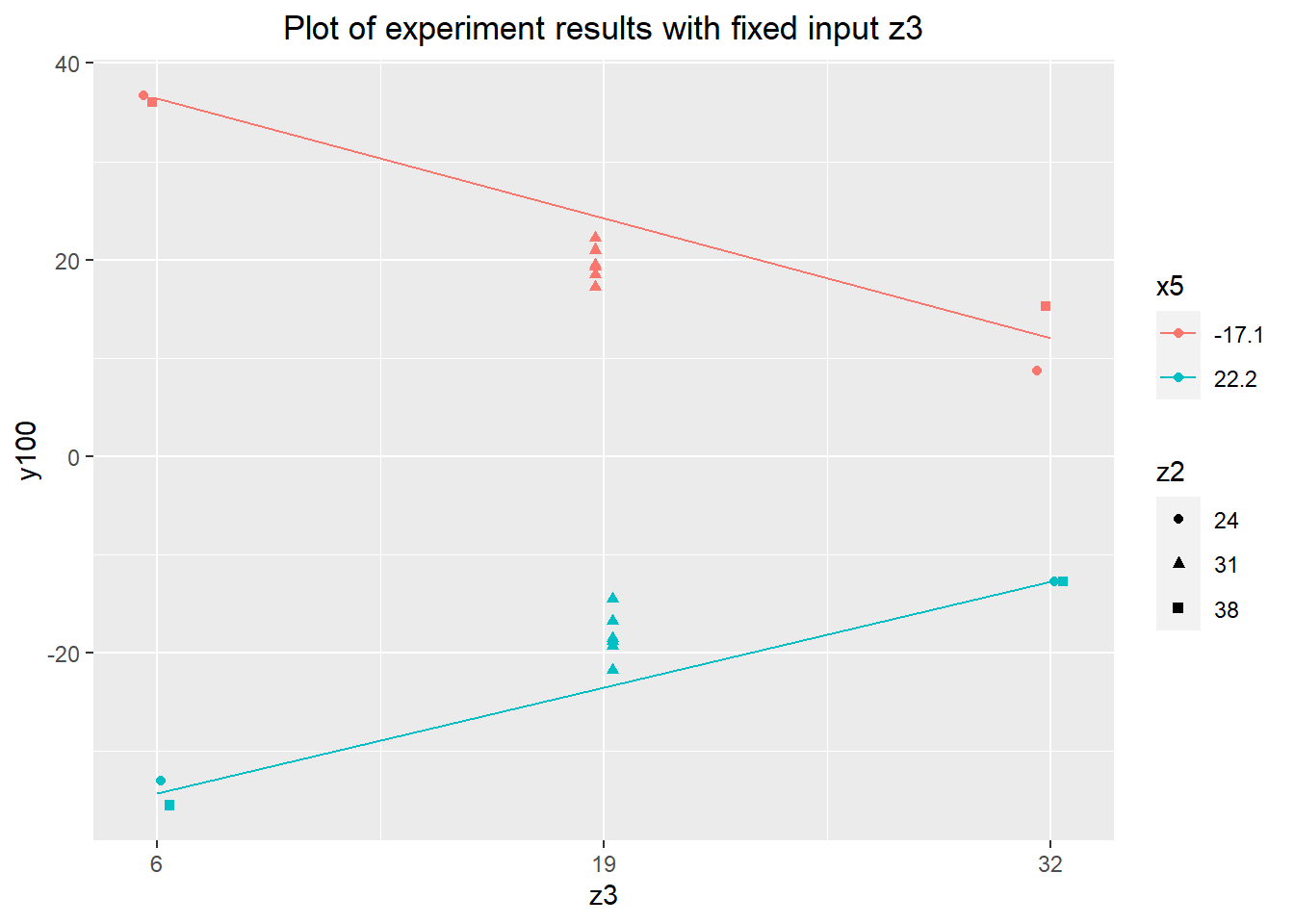
Further Investigation
A second experiment was performed to better quantify the effect of z3 on the output. The plan was to run the experiment over five levels of x5 spanning its expected range. The cost of implementing z3 as a desensitizer depends on its level, with the cost proportional to the square of its difference from the default value of 19. This makes exploring more modest values of z3 worthwhile, so both the extreme value of 32 and the less extreme value of 22.5 were used. This was run as a full factorial experiment with 2 fixed levels of z3 and 5 fixed levels of x5, and 2 replications each.
desen.quant.data <- read.delim("desensitizer-z3.tsv")
summary(desen.quant.data)## daycount shift partnum y100 y300
## Min. :7.00 Min. :1.0 Min. : 9601 Min. :-6.750 Min. :-8.00
## 1st Qu.:7.75 1st Qu.:1.0 1st Qu.: 9966 1st Qu.:-4.875 1st Qu.:-1.75
## Median :8.00 Median :1.0 Median :10090 Median : 0.375 Median : 0.25
## Mean :7.75 Mean :1.5 Mean : 9970 Mean : 0.550 Mean : 0.25
## 3rd Qu.:8.00 3rd Qu.:1.5 3rd Qu.:10095 3rd Qu.: 4.938 3rd Qu.: 1.00
## Max. :8.00 Max. :3.0 Max. :10100 Max. : 9.750 Max. : 9.75
## NA's :15
## z3 x5
## Min. :22.50 Min. :-10.00
## 1st Qu.:22.50 1st Qu.: -3.75
## Median :27.25 Median : 2.50
## Mean :27.25 Mean : 2.50
## 3rd Qu.:32.00 3rd Qu.: 8.75
## Max. :32.00 Max. : 15.00
## desen.quant.dataJust to be certain that z3 doesn't have significant downstream effects on y300 (which are not captured by measuring y100), the first 5 runs of the experiment measured both y100 and y300. The results are shown below: there doesn't appear to be much difference between the y100 and y300 values, similar to the verification experiment. A regression model predicting y300 from y100 also gives a similar result, with the predicted y300 being close to the value of y100. This tells us that our previously established model of the process should still hold.
melt(desen.quant.data[!is.na(desen.quant.data$y300),],
variable.name="y", measure.vars=c("y100", "y300"))ggplot(data=melt(desen.quant.data[!is.na(desen.quant.data$y300),],
variable.name="y", measure.vars=c("y100", "y300"))) +
geom_point(aes(x=x5, y=value, color=y, shape=y), size=1.8, position=position_dodge(0.5)) +
labs(title="Plot of y100 and y300 for z3 = 32",
y="Output") +
scale_color_discrete(name="") +
scale_shape_discrete(name="") +
theme(plot.title=element_text(hjust=0.5))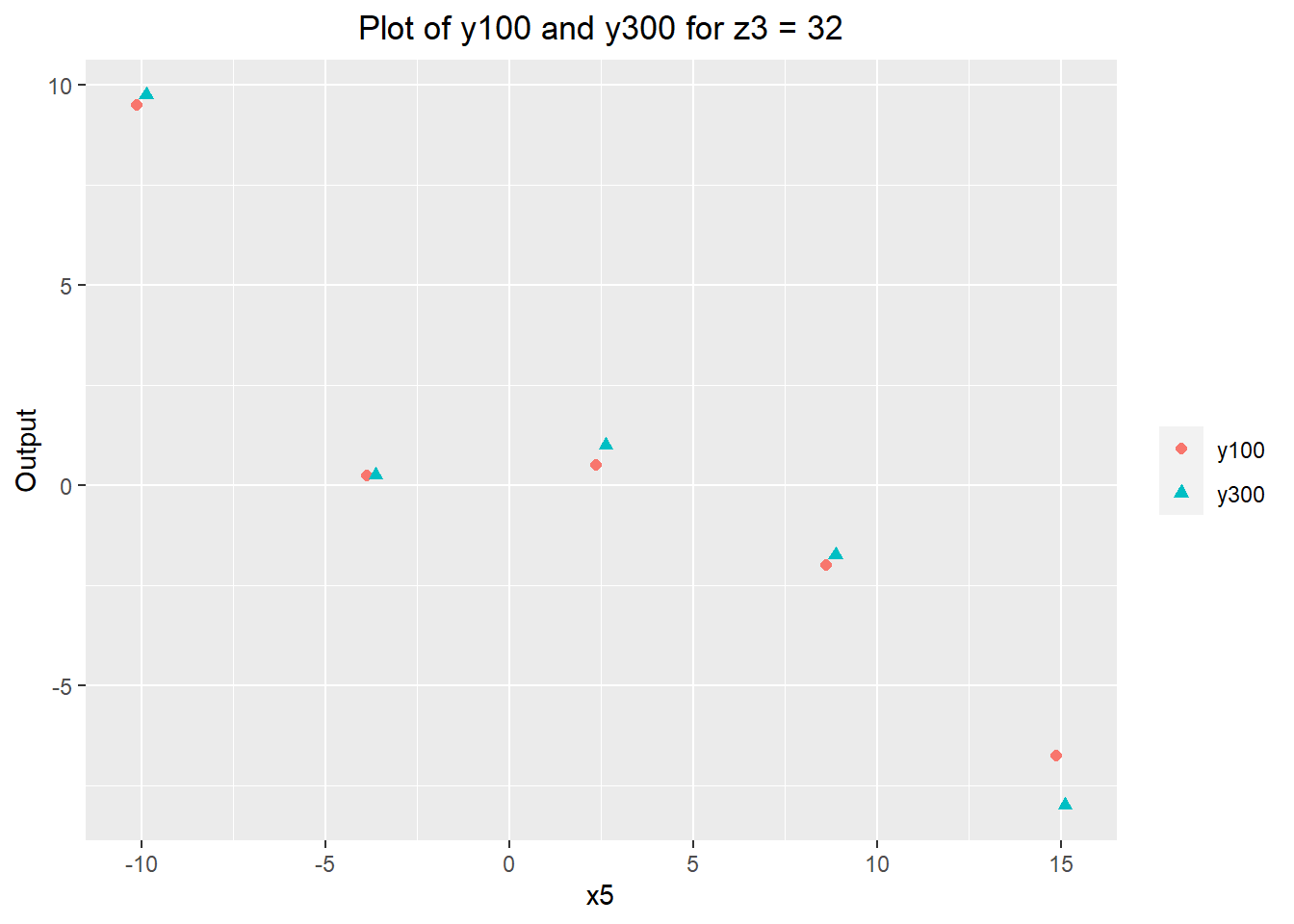
summary(lm(y300~y100, data=desen.quant.data))##
## Call:
## lm(formula = y300 ~ y100, data = desen.quant.data)
##
## Residuals:
## 1 2 3 4 5
## -0.40066 0.05381 0.53477 0.47517 -0.66308
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.07285 0.27306 -0.267 0.806926
## y100 1.07616 0.05158 20.863 0.000241 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6096 on 3 degrees of freedom
## (15 observations deleted due to missingness)
## Multiple R-squared: 0.9932, Adjusted R-squared: 0.9909
## F-statistic: 435.3 on 1 and 3 DF, p-value: 0.0002408To get a picture of the desensitizing effect, the experimental results were compared with the observations from the group comparison investigation. There does seem to be an effect, but it's fairly modest. This assessment is backed up by a regression model using the 3 levels of z3 as factors. The model presents the new levels of z3 decreasing the magnitude of the effect of x5 on y100 by about 37%, from -0.99 to -0.63. Interestingly, there is no discernible difference in effect between the two new levels of z3 -- they both appear to desensitize the process equally well.
Additionally, there doesn't appear to be a significant difference in the model intercept, with a 95% confidence interval of [-2.67, 0.46]. This is probably small enough to not need an adjuster to correct any off-center-ness in the new process, which reduces both the cost and complexity of the solution.
ggplot(desen.quant.data) +
geom_point(aes(x=x5, y=y100, color=as.factor(z3)),
position=position_jitter(width=0.2, height=0)) +
geom_point(aes(x=x5, y=y100), data=groups.data, color="#303030", size=1) +
labs(title="Plot of experiment results for different z3\n(grey dots are previous observations with z3=19)") +
geom_hline(yintercept=min(baseline.data$y100)) +
geom_hline(yintercept=max(baseline.data$y100)) +
scale_color_discrete(name="z3") +
theme(plot.title=element_text(hjust=0.5)) +
scale_x_continuous(breaks=seq(-10, 15, length.out=5))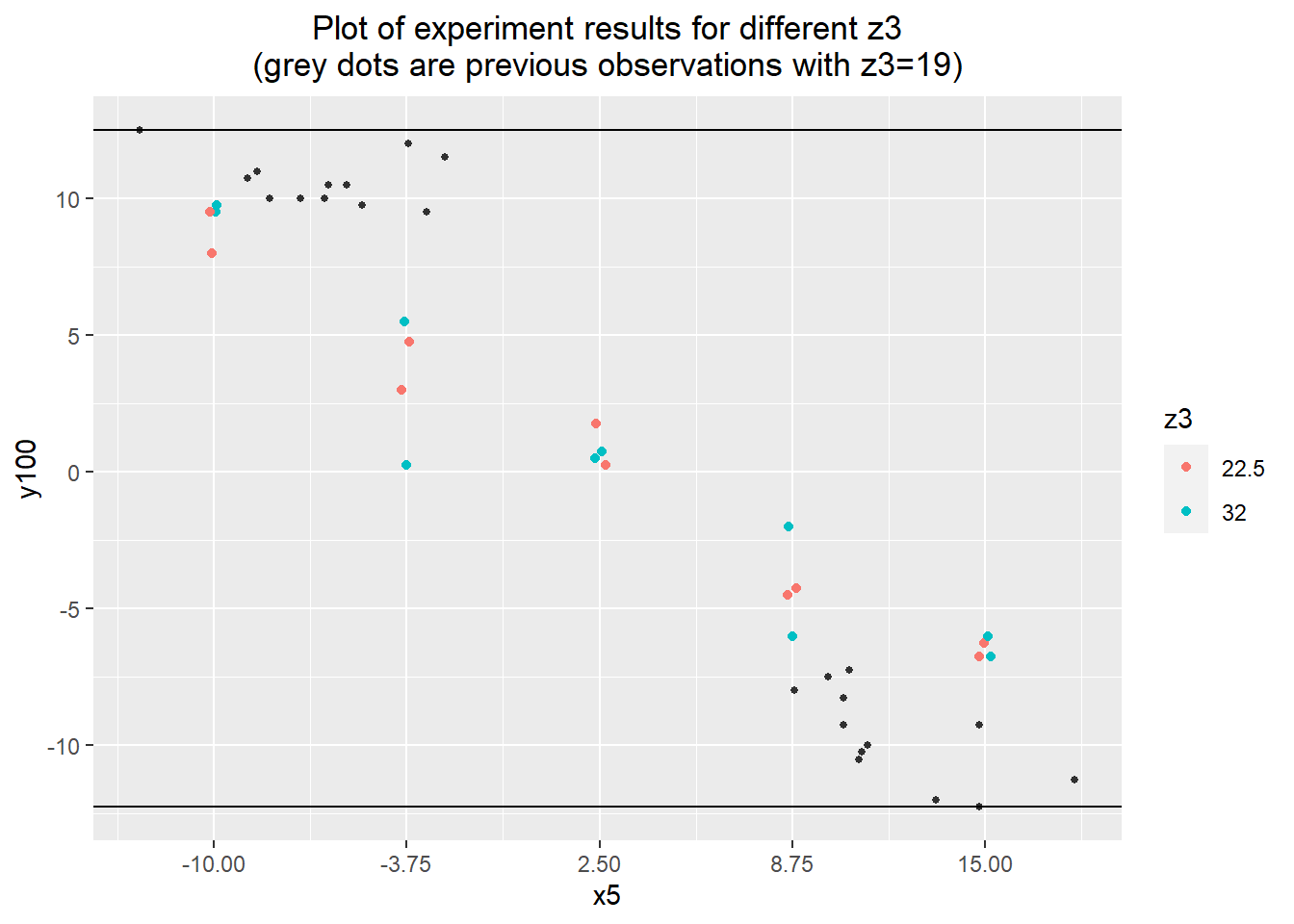
desen.data.aug <- rbind(verif.data[,c("y100", "x5")], groups.data[,c("y100", "x5")])
desen.data.aug$z3 <- 19
desen.data.aug <- rbind(desen.data.aug, desen.quant.data[,c("y100", "x5", "z3")])
summary(desen.data.aug)## y100 x5 z3
## Min. :-21.7500 Min. :-17.100 Min. :19.00
## 1st Qu.: -8.5000 1st Qu.: -7.450 1st Qu.:19.00
## Median : 0.3750 Median : 2.500 Median :19.00
## Mean : 0.5625 Mean : 2.616 Mean :21.95
## 3rd Qu.: 10.0000 3rd Qu.: 11.750 3rd Qu.:22.50
## Max. : 22.2500 Max. : 22.200 Max. :32.00z3.full.model <- lm(y100 ~ x5*as.factor(z3), data=desen.data.aug)
summary(z3.full.model)##
## Call:
## lm(formula = y100 ~ x5 * as.factor(z3), data = desen.data.aug)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.1875 -1.2612 -0.0545 1.2000 5.8187
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.21443 0.36578 8.788 1.03e-11 ***
## x5 -0.98673 0.02602 -37.923 < 2e-16 ***
## as.factor(z3)22.5 -1.11443 0.79691 -1.398 0.168
## as.factor(z3)32 -1.10943 0.79691 -1.392 0.170
## x5:as.factor(z3)22.5 0.36673 0.08135 4.508 3.96e-05 ***
## x5:as.factor(z3)32 0.36473 0.08135 4.483 4.30e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.154 on 50 degrees of freedom
## Multiple R-squared: 0.9691, Adjusted R-squared: 0.966
## F-statistic: 313.6 on 5 and 50 DF, p-value: < 2.2e-16Investigation 6 – Adjuster
In the previous investigation, we found that z1 appears to be our best candidate adjuster. To make use of z1 in an active control scheme, we need to have a good estimate of the relationship between z1 and y100 (and y300). Like with the desensitizer z3, we need to do a more in-depth investigation. This took the form of an experiment varying z1 at its two extremes: 68 and 94. As with z3, several runs (the first 10) measured both y100 and y300, and the remainder (10 more) just measured y100 to save on costs. x5 was also measured, to provide a diagnosis tool in case the results did not turn out as expected.
adjuster.data <- read.delim("adjuster-z1.tsv")
summary(adjuster.data)## daycount shift partnum y100 y300
## Min. :8 Min. :2.0 Min. :10561 Min. :-12.000 Min. :-11.750
## 1st Qu.:8 1st Qu.:2.0 1st Qu.:10566 1st Qu.: -7.750 1st Qu.: -7.562
## Median :8 Median :2.5 Median :10806 Median : -0.375 Median : -1.875
## Mean :8 Mean :2.5 Mean :10806 Mean : 1.438 Mean : 0.875
## 3rd Qu.:8 3rd Qu.:3.0 3rd Qu.:11045 3rd Qu.: 8.625 3rd Qu.: 8.688
## Max. :8 Max. :3.0 Max. :11050 Max. : 17.750 Max. : 17.250
## NA's :10
## z1 x5
## Min. :68 Min. :-3.40
## 1st Qu.:68 1st Qu.:-1.40
## Median :81 Median : 1.65
## Mean :81 Mean : 1.78
## 3rd Qu.:94 3rd Qu.: 3.00
## Max. :94 Max. : 9.90
## It looks like there may be a higher variability in y300 at the low levels of z1, but the linear fit for y300 based on y100 is consistent between all 3 levels of z1. It seems likely that more samples of both y100 and y300 are needed to properly assess the potential impact of z1, but at the time I moved forward with the remainder of the investigation.
ggplot(data=melt(adjuster.data[!is.na(adjuster.data$y300),],
variable.name="y", measure.vars=c("y100", "y300"))) +
geom_point(aes(x=x5, y=value, color=y, shape=y), size=1.8) +
labs(title="Plot of observed y100 and y300 from adjuster investigation",
y="Output") +
scale_color_discrete(name="") +
scale_shape_discrete(name="") +
theme(plot.title=element_text(hjust=0.5))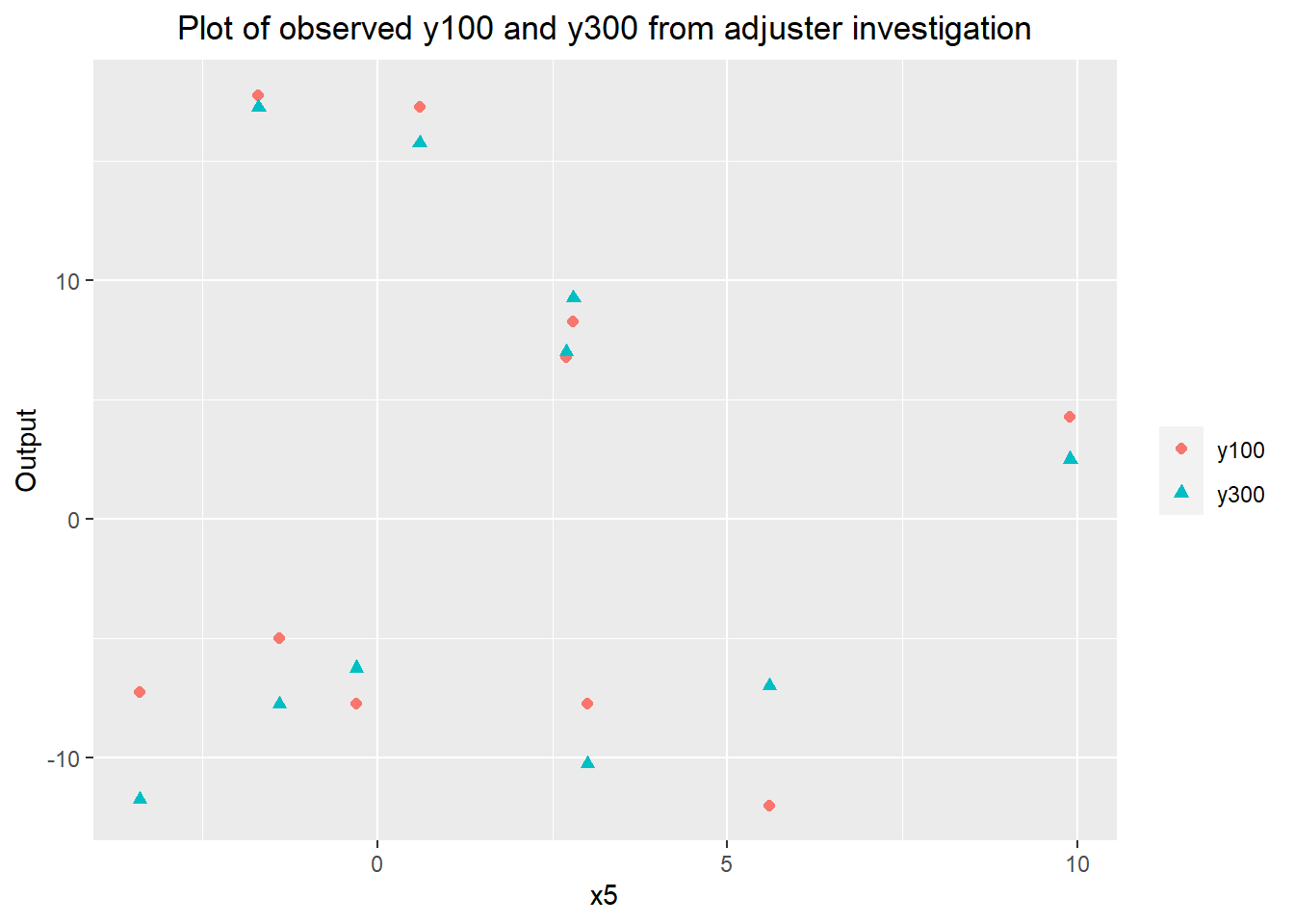
ggplot(adjuster.data) + geom_point(aes(x=y100, y=y300, color=as.factor(z1))) +
scale_color_discrete(name="z1") +
labs(title="Plot of y100-y300 relationship at high and low z1") +
theme(plot.title = element_text(hjust=0.5))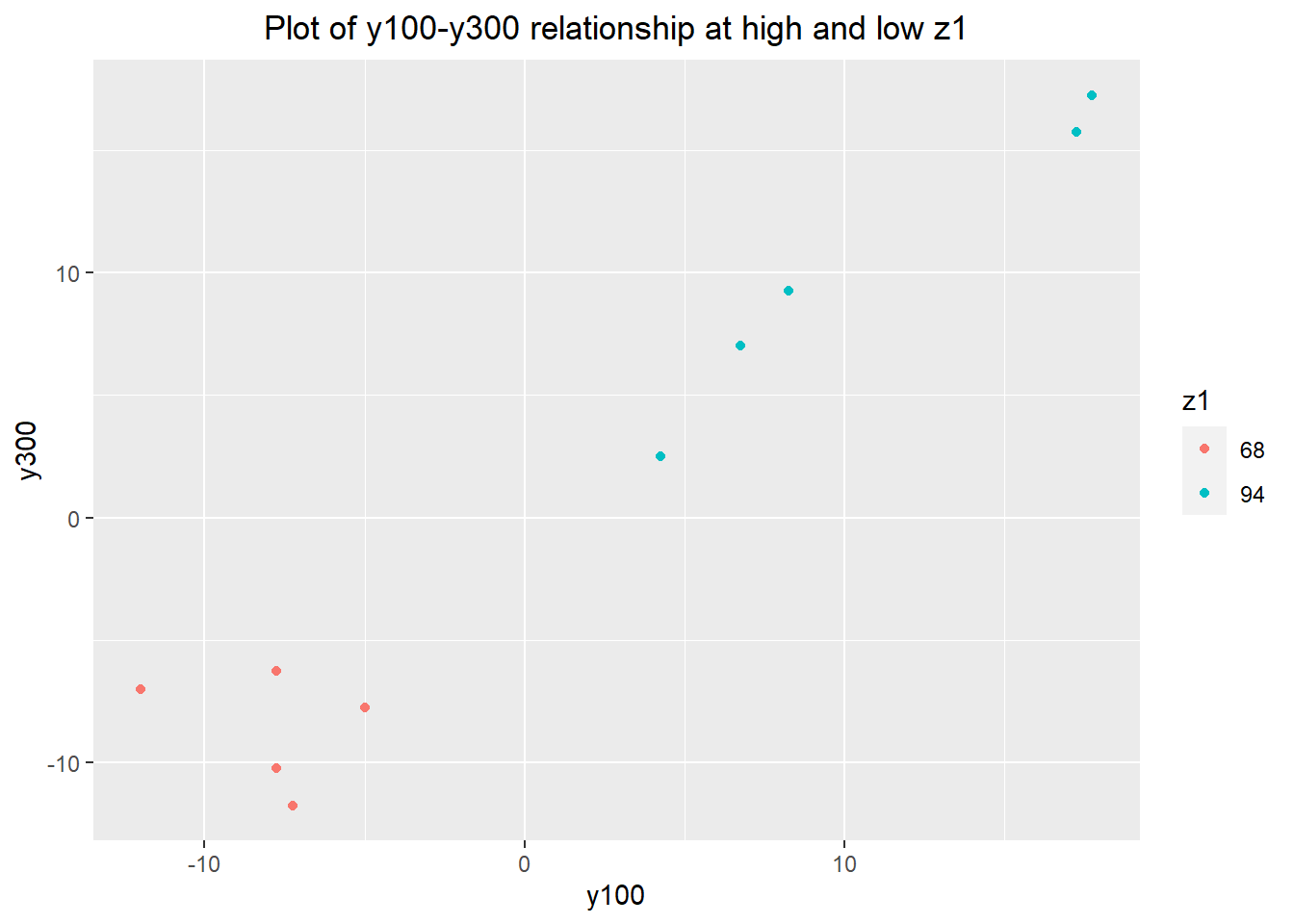
y300.y100.z1.model <- lm(y300~y100 + y100:as.factor(z1), data=adjuster.data)
summary(y300.y100.z1.model)##
## Call:
## lm(formula = y300 ~ y100 + y100:as.factor(z1), data = adjuster.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.175 -1.599 -0.079 1.913 3.656
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.8720 2.3448 -1.225 0.2603
## y100 0.6487 0.3119 2.080 0.0761 .
## y100:as.factor(z1)94 0.5173 0.4798 1.078 0.3167
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.796 on 7 degrees of freedom
## (10 observations deleted due to missingness)
## Multiple R-squared: 0.9489, Adjusted R-squared: 0.9343
## F-statistic: 64.95 on 2 and 7 DF, p-value: 3.023e-05I used an F-test (Levene's test) to compare the residuals between the two different z1 values. The variance of the low z1 (\(z_1 = 68\)) group is quite a bit higher than the high z1 group - our F-statistic is 3.53. However, with only 10 observations in total, the acceptance region for the F-test spans almost two orders of magnitude ([0.104, 9.604]) -- statistics is saying we don't have a large enough sample size. This translates to a 95% confidence interval for the true ratio of variances of [0.37, 33.87]. It may have been worthwhile to take the extra cost and measure more y300 values to increase our certainty that z1 was not having a downstream effect on y300. However, having a sense of the way the game was implemented, and knowing that any increase in variance would not be huge compared to the other process variability, it seemed relatively safe to save on costs and just measure y100 for the remaining 10 parts.
var(y300.y100.z1.model$residuals[(adjuster.data$z1 == 68) & !is.na(adjuster.data$y300)],
na.rm=TRUE) /
var(y300.y100.z1.model$residuals[(adjuster.data$z1 == 94) & !is.na(adjuster.data$y300)],
na.rm=TRUE)## [1] 3.526709qf(c(0.025, 0.975),
sum((adjuster.data$z1 == 68) & !is.na(adjuster.data$y300)) - 1,
sum((adjuster.data$z1 == 94) & !is.na(adjuster.data$y300)) - 1)## [1] 0.1041175 9.6045299Using the experimental results along with the results of the group comparison and dominant cause verification, we can get a good sense of the relationship between z1, x5, and y100. z1 appears to have good performance as an adjuster, and over its two extremes it seems to be able to adjust the level of y100 by 20.
adjuster.data.aug <- rbind(groups.data[,c("y100", "x5")], verif.data[,c("y100", "x5")])
adjuster.data.aug$z1 <- 81
adjuster.data.aug <- rbind(adjuster.data.aug, adjuster.data[,c("y100", "x5", "z1")])
adjuster.data.aug$z1.cent <- adjuster.data.aug$z1 - 81
ggplot(data=adjuster.data.aug) +
geom_point(aes(x=x5, y=y100, color=as.factor(z1), shape=as.factor(z1))) +
stat_smooth(aes(x=x5, y=y100, color=as.factor(z1)), method="lm") +
labs(title="Adjuster experiment results\n(including previous investigations)") +
scale_color_discrete(name="z1") +
scale_shape_discrete(name="z1") +
theme(plot.title=element_text(hjust=0.5))## `geom_smooth()` using formula 'y ~ x'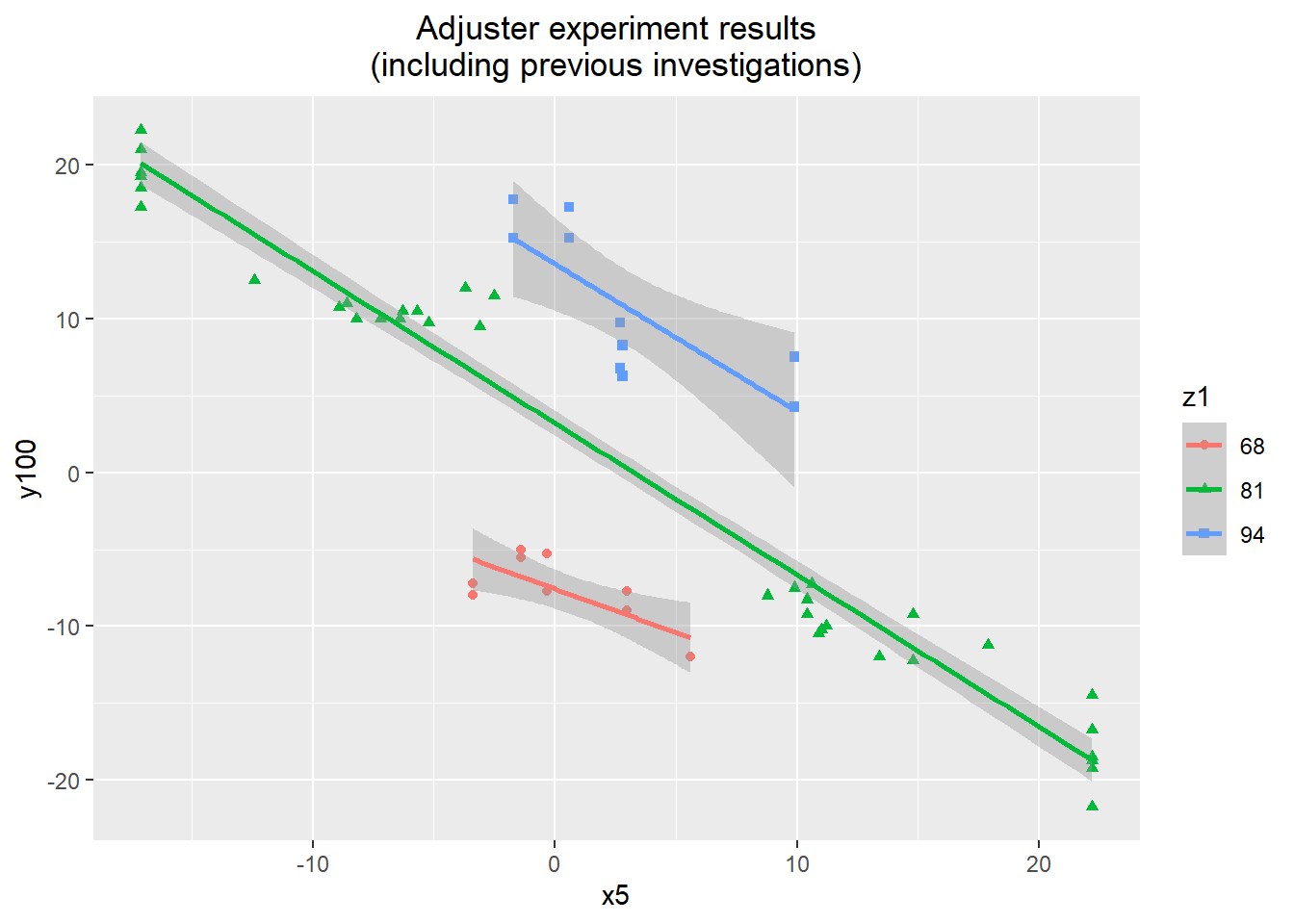
Fitting a linear regression model confirms this. To make clear any difference in the x5-y100 relationship at different levels of z1, the level of z1 was coded as a factor. There is a lot of variability in the estimates for the different x5-y100 relationships at the different levels of z1. This may be due to the small sample size, but there is at least strong evidence to indicate that the relationship is the same for the middle and upper values of z1 (81 and 94). There could be an argument that this warrants more observations at the lower level of z1, but including the (admittedly limited) evidence from the screening investigation, it felt safe to attribute the small difference to noise.
summary(lm(y100~x5*as.factor(z1), data=adjuster.data.aug))##
## Call:
## lm(formula = y100 ~ x5 * as.factor(z1), data = adjuster.data.aug)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.6325 -1.5981 -0.3436 1.6851 5.8187
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.5522 0.7972 -9.474 9.59e-13 ***
## x5 -0.5682 0.2426 -2.342 0.0232 *
## as.factor(z1)81 10.7667 0.9002 11.961 2.78e-16 ***
## as.factor(z1)94 21.1186 1.2533 16.851 < 2e-16 ***
## x5:as.factor(z1)81 -0.4185 0.2445 -1.712 0.0931 .
## x5:as.factor(z1)94 -0.3903 0.3147 -1.240 0.2207
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.463 on 50 degrees of freedom
## Multiple R-squared: 0.966, Adjusted R-squared: 0.9626
## F-statistic: 284.2 on 5 and 50 DF, p-value: < 2.2e-16Having determined that the interaction between z1 and x5 is not significant, I fit a linear model just using the values of x5 and z1 as predictors. To make the model more interpretable, I centred the z1 predictor so that it described how deviations of z1 from its default value impact the output y100. We get an x5 coefficient that's compatible with our previous estimates (this is our largest sample for predicting the x5-y100 relationship yet), and a strong effect of z1 on y100. The coefficient of 0.804 on z1 means that it could be used to control over 80% of the entire observed range of y100, if we have a good means to predict y100.
summary(lm(y100~x5 + z1.cent, data=adjuster.data.aug))##
## Call:
## lm(formula = y100 ~ x5 + z1.cent, data = adjuster.data.aug)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.6431 -1.6022 -0.1188 1.7136 5.8586
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.19132 0.33607 9.496 4.97e-13 ***
## x5 -0.98004 0.02917 -33.595 < 2e-16 ***
## z1.cent 0.80353 0.04241 18.946 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.462 on 53 degrees of freedom
## Multiple R-squared: 0.964, Adjusted R-squared: 0.9626
## F-statistic: 709.7 on 2 and 53 DF, p-value: < 2.2e-16Due to the way the investigations were conducted, this is actually our first random sample of x5 from normal operation of the process. With the y100 baseline concluding that y100 fits a normal distribution, the strong relationship between x5 and y100 indicates x5 probably has a rough normal distribution as well. We don't have many observations, so any test of normality is going to be very rough, but a shapiro-wilk test provides a p-value of 0.0858. Using this test result and the intuition from the relationship with the much better observed y100, characterizing x5 with a normal distribution seems reasonable.
ggplot(adjuster.data) + geom_qq(aes(sample=x5)) +
geom_qq_line(aes(sample=x5)) +
labs(title="Normal Quantile plot of observed x5",
y="x5") +
theme(plot.title = element_text(hjust=0.5))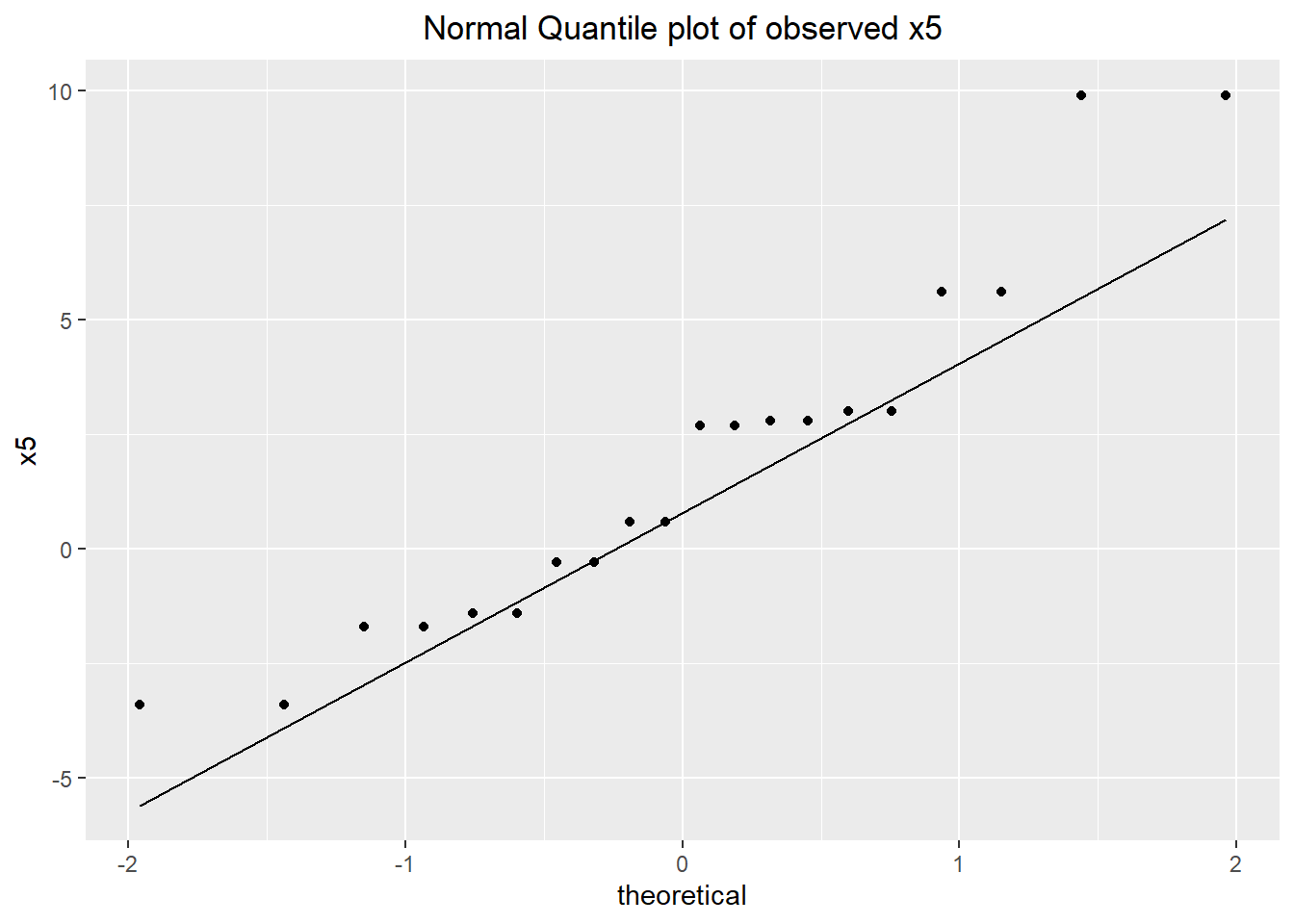
shapiro.test(adjuster.data$x5)##
## Shapiro-Wilk normality test
##
## data: adjuster.data$x5
## W = 0.91675, p-value = 0.0858The observed data have a mean of 1.78 and a standard deviation of 3.82. This roughly fits the observed extreme values of x5 seen in the retrospective investigation of the baseline (if anything, the standard deviation seems somewhat low).
var(adjuster.data$x5)## [1] 14.59747sd(adjuster.data$x5)## [1] 3.820664mean(adjuster.data$x5)## [1] 1.78Using all the data we have collected including observations of both y100 and y300, we can get our best estimate yet of the relationship between y100 and y300. In the setup to this problem, our team supposedly did a fairly thorough investigation of the relationship between the intermediate outputs and the final output y300, but I guess that information is lost. This model indicates that on average the value of y300 for a part can be best predicted by its y100 value (0.991 times it), with a residual standard deviation of 2.095. This will factor into our estimations in the final section of the variation reduction process.
summary(lm(y300~y100,
data=rbind(adjuster.data[!is.na(adjuster.data$y300),c("y100", "y300")],
desen.quant.data[!is.na(desen.quant.data$y300),c("y100", "y300")],
verif.data[,c("y100", "y300")])))##
## Call:
## lm(formula = y300 ~ y100, data = rbind(adjuster.data[!is.na(adjuster.data$y300),
## c("y100", "y300")], desen.quant.data[!is.na(desen.quant.data$y300),
## c("y100", "y300")], verif.data[, c("y100", "y300")]))
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.4613 -1.2252 -0.2257 0.5226 4.9964
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.1031 0.4040 -0.255 0.801
## y100 0.9911 0.0281 35.273 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.095 on 25 degrees of freedom
## Multiple R-squared: 0.9803, Adjusted R-squared: 0.9795
## F-statistic: 1244 on 1 and 25 DF, p-value: < 2.2e-16Investigation 7 – Assessment and Implementation of Solution Approach
Approach evaluation
Having determined which input is the dominant cause of observed variation in the process output, and finding fixed inputs which could be used as a desensitizer and adjuster, we can compare the variation reduction approaches which are available to us.
Three approaches are infeasible right off the bat:
Feedback control is an approach which uses previous measured values of the output to change the level of the adjuster. The value of our output of interest changes substantially between each part, so feedback control is more likely to increase variation than reduce it.
"Fix the obvious" solves the problem at its source by attempting to reduce variation in the dominant cause. For whatever reason, the game's documentation says that the dominant cause (x5) cannot have its variation reduced. This might be unrealistic, but we'll take it at its word.
Process robustness is basically the name given to a desensitization approach when the dominant cause is not known. Instead of investigating the effect of inputs on the known range of the dominant cause, we're searching blindly for an input we can change which reduces variation in the process. We know the dominant cause, and information about that gave us a desensitizer, so I guess you could also say the two solution approaches are equivalent at this point.
There are three remaining approaches: 100% inspection, feedforward control, and desensitization. Below I explain what they are and compare their costs and benefits.
100% Inspection
This approach basically solves the variation problem by measuring each part as it is being produced, and scrapping any parts which fall out of spec. This has the benefit that the variation down the line is reduced, but the measurement and scrapping is quite costly. As we saw in the baseline, the process did not appear to have a systematic pattern of variation in the mean or variance, so a less intensive scheme like acceptance sampling would not be able to reduce variation in the output.
To assess 100% inspection as an approach, I generated a big sample of parts based on the data we've collected over the course of the investigations. We first generate a bunch of x5, then use the linear x5-y100 relationship to generate a bunch of y100 values, then use the linear y100-y300 relationship to generate a bunch of y300 values. We can then see what the rejection rate and final output are like under different inspection schemes.
sim_y100 <- function(x5, z1=0) {
predicted <- -0.9800*x5 + 0.8035*z1 + 3.1913
sim <- predicted + rnorm(length(predicted), sd=2.462)
return(sim)
}
sim_y300 <- function(y100) {
predicted <- 0.9911*y100 - 0.1031
sim <- predicted + rnorm(length(predicted), sd=2.095)
return(sim)
}
x5 <- rnorm(20000, mean=1.78, sd=3.82)
y100 <- sim_y100(x5)
y300 <- sim_y300(y100)I considered two families of prediction schemes: one looking at x5, and one looking at the intermediate output of the preassembly (step 100). The most reasonable behaviour would be to use the measured values to predict y300, and reject the part if the predicted y300 goes outside some "safe" range. The code below does that, looping through threshold y300 values and saving the rejection/scrap rate, and the standard deviation of the parts which passed.
predicted.y300.x5 <- -0.971*x5 + 3.059
predicted.y300.y100 <- 0.9911*y100 - 0.1031
thresholds <- seq(0, 15, length.out=31)
x5.prop.scrapped <- c()
x5.sd <- c()
x5.oospec <- c()
y100.prop.scrapped <- c()
y100.sd <- c()
y100.oospec <- c()
for(threshold in thresholds)
{
x5.pred.scrap <- abs(predicted.y300.x5) > threshold
x5.prop.scrapped <- c(x5.prop.scrapped, mean(x5.pred.scrap))
x5.remaining <- y300[!x5.pred.scrap]
x5.sd <- c(x5.sd, sd(x5.remaining))
x5.oospec <- c(x5.oospec, mean(abs(x5.remaining)>10))
y100.pred.scrap <- abs(predicted.y300.y100) > threshold
y100.remaining <- y300[!y100.pred.scrap]
y100.prop.scrapped <- c(y100.prop.scrapped, mean(y100.pred.scrap))
y100.sd <- c(y100.sd, sd(y100.remaining))
y100.oospec <- c(y100.oospec, mean(abs(y100.remaining) > 10))
}The results made intuitive sense. At each threshold, the x5 predictor resulted in fewer parts scrapped than the y100 predictor, with all parts scrapped when the threshold was zero, and no parts scrapped when the threshold was 15.
ggplot() +
geom_line(aes(x=thresholds, y=x5.prop.scrapped), color="red") +
geom_line(aes(x=thresholds, y=y100.prop.scrapped), color="blue") +
labs(title="Proportion of parts scrapped under 100% inspection\nusing x5 predictor (red) and y100 predictor (blue)",
x="Predicted y300 Threshold",
y="Proportion scrapped") +
theme(plot.title=element_text(hjust=0.5)) 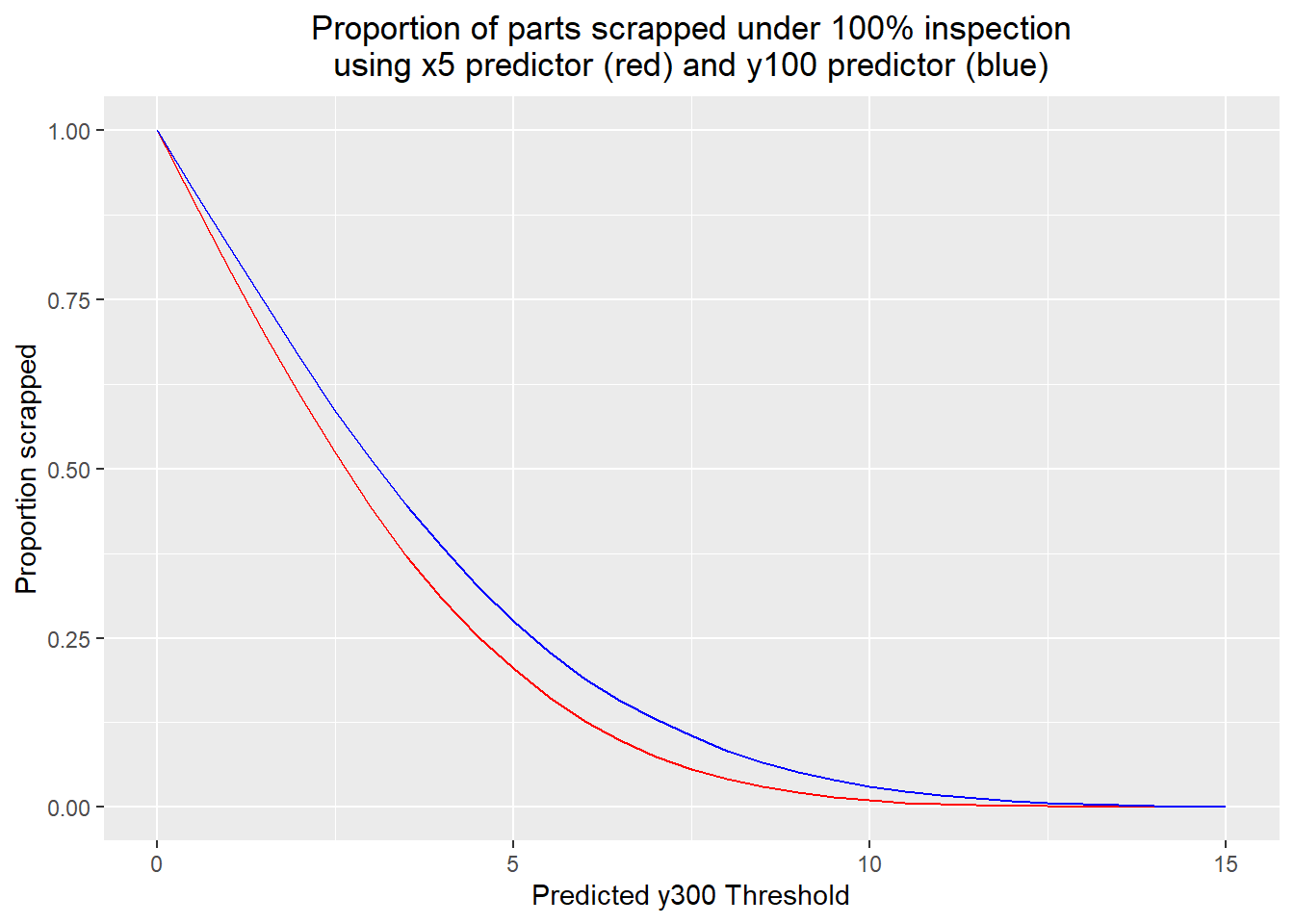
The output standard deviations also made sense, again because of the extra variation in y100 not due to x5.
ggplot() +
geom_line(aes(x=thresholds, y=x5.sd), color="red") +
geom_line(aes(x=thresholds, y=y100.sd), color="blue") +
labs(title="Output standard deviation under 100% inspection\nusing x5 predictor (red) and y100 predictor (blue)",
x="Predicted y300 Threshold",
y="Standard deviation") +
theme(plot.title=element_text(hjust=0.5)) 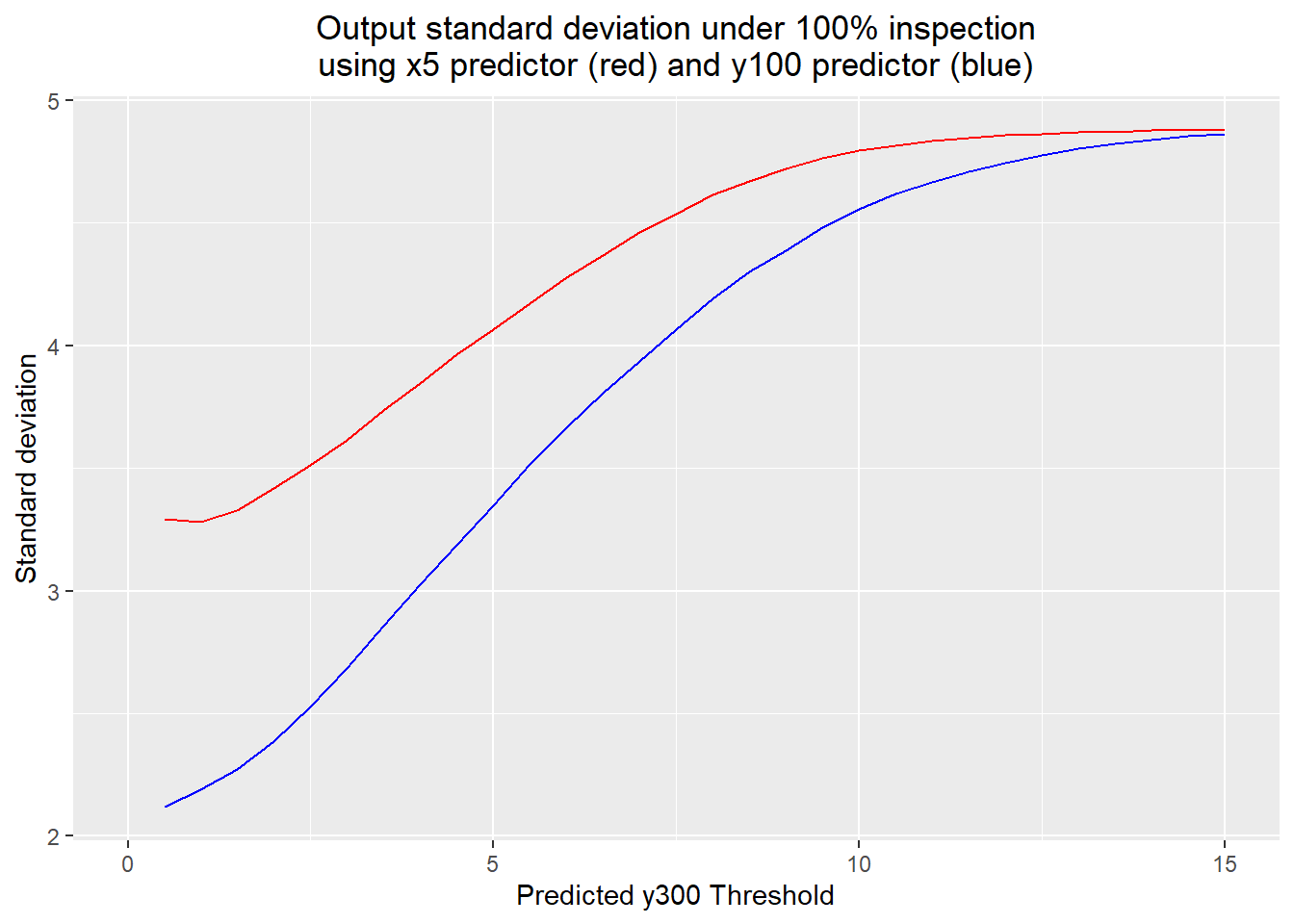
ggplot() +
geom_line(aes(x=thresholds, y=x5.oospec), color="red") +
geom_line(aes(x=thresholds, y=y100.oospec), color="blue") +
labs(title="Proportion of parts scrapped under 100% inspection\nusing x5 predictor (red) and y100 predictor (blue)",
x="Predicted y300 Threshold",
y="Proportion scrapped") +
theme(plot.title=element_text(hjust=0.5)) 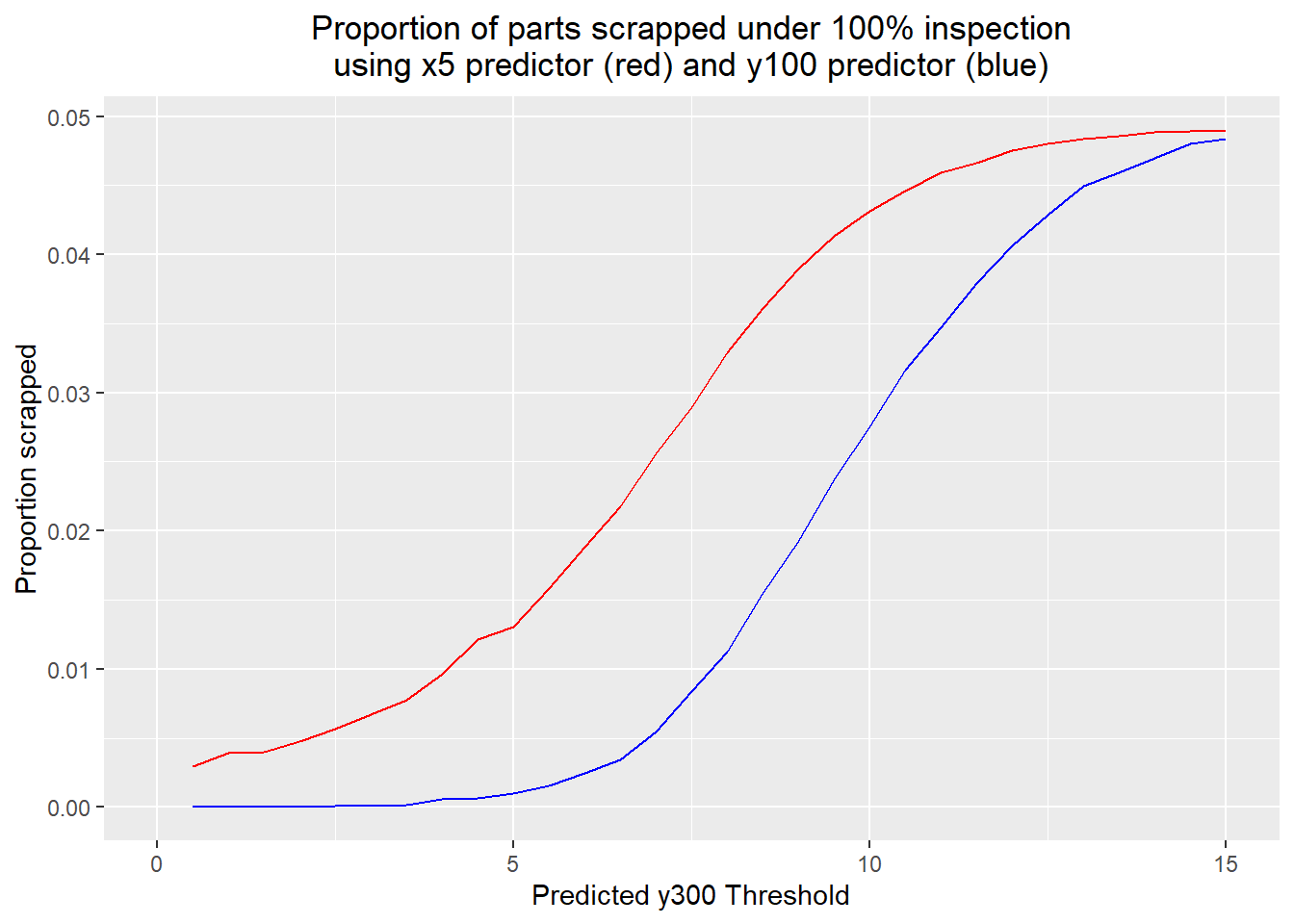
x5.costs <- 5*x5.prop.scrapped + 0.3
y100.costs <- 40*y100.prop.scrapped + 1
x5.quality <- 25 * (1 - (x5.sd/5)^2)
y100.quality <- 25 * (1 - (y100.sd/5)^2)The actual cost/benefit results using the implementation costs and cost savings due to variation reduction were fairly counterintuitive. This found that x5 was the better predictor to use, and that the optimum threshold would be 1.5: an input component would be rejected if its measured x5 predicted a y300 outside the range [-1.5, 1.5]. In the simulation, about 70% of components were scrapped under this scheme, although the standard deviation of the output was reduced to 3.32 and only 0.40% of output parts were out of spec; more than an order of magnitude less than without the inspection process. In contrast, the best threshold using the y100 predictor was 7. Here, 13% of parts were scrapped; the standard deviation of the output parts is 3.93, and 0.54% of output parts are out of spec.
When the costs are calculated, the x5 inspection vastly outperforms the y100 inspection. The x5 inspection has an average net benefit of $10.14 per part, while the y100 inspection has an average net benefit of $3.31 per part. This difference boils down to the significant increase in value put into the part in the preassembly step: measuring and throwing out 70% of one of the input components has the same cost as measuring and throwing out 7% of the preassembled parts.
x5.best <- which.max(x5.quality-x5.costs)
thresholds[x5.best]## [1] 1.5x5.prop.scrapped[x5.best]## [1] 0.6997x5.sd[x5.best]## [1] 3.325955x5.oospec[x5.best]## [1] 0.003996004(x5.quality-x5.costs)[x5.best]## [1] 10.13953ggplot() +
geom_line(aes(x=thresholds, y=x5.costs), color="red") +
geom_line(aes(x=thresholds, y=x5.quality), color="blue") +
geom_line(aes(x=thresholds, y=(x5.quality-x5.costs)), color="black") +
labs(title="Quality Savings (blue), Cost (red), and Net Benefit (black)\nof 100% inspection simulations using x5",
x="Predicted y300 Threshold",
y="Cost/Benefit ($)") +
theme(plot.title=element_text(hjust=0.5)) 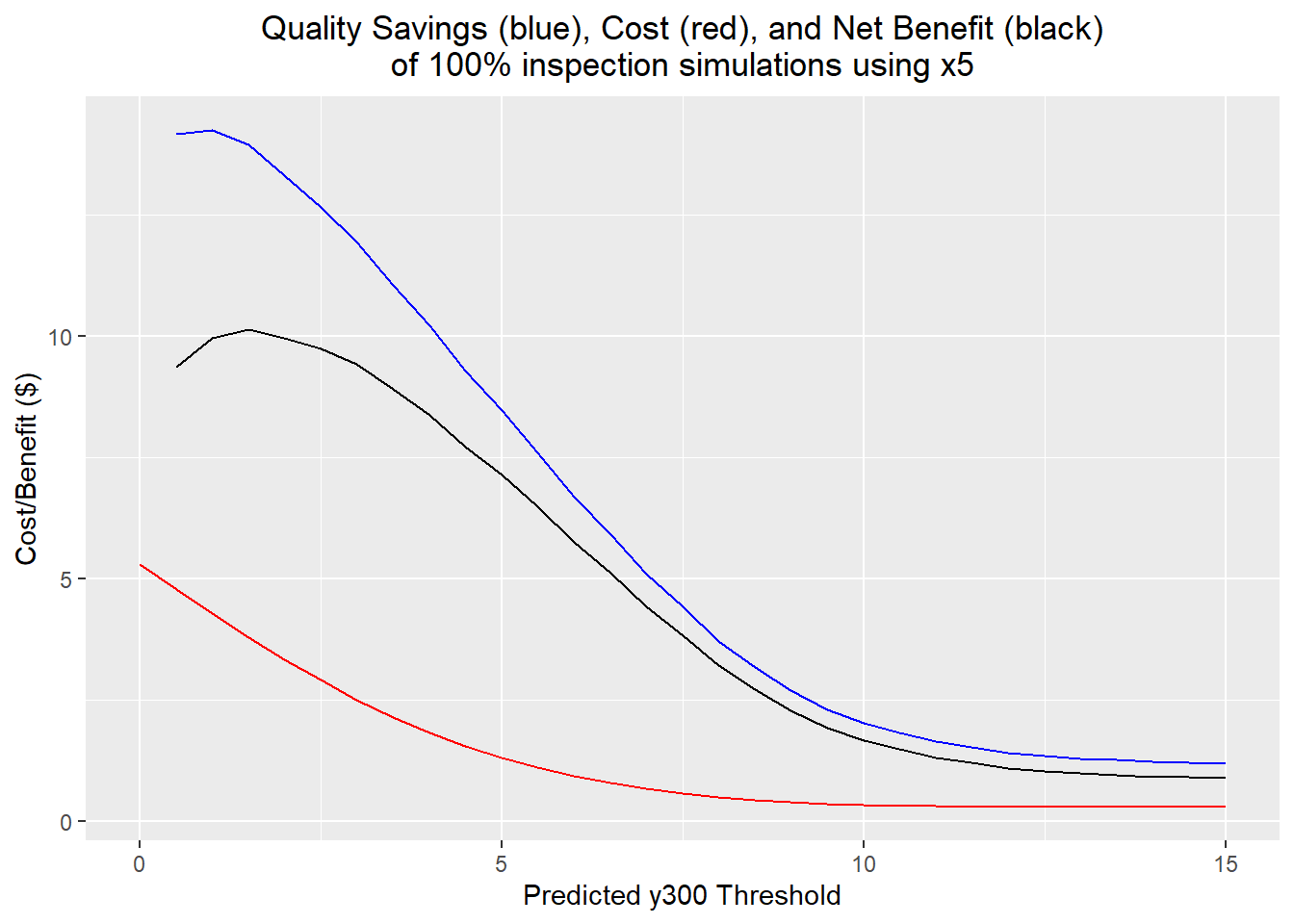
y100.best <- which.max(y100.quality-y100.costs)
thresholds[y100.best]## [1] 7y100.prop.scrapped[y100.best]## [1] 0.12955y100.sd[y100.best]## [1] 3.937474(y100.quality-y100.costs)[y100.best]## [1] 3.314299y100.oospec[y100.best]## [1] 0.005456948ggplot() +
geom_line(aes(x=thresholds, y=y100.costs), color="red") +
geom_line(aes(x=thresholds, y=y100.quality), color="blue") +
geom_line(aes(x=thresholds, y=(y100.quality-y100.costs)), color="black") +
labs(title="Quality Savings (blue), Cost (red), and Net Benefit (black)\nof 100% inspection simulations using y100",
x="y300 Threshold",
y="Cost/Benefit ($)") +
theme(plot.title=element_text(hjust=0.5)) 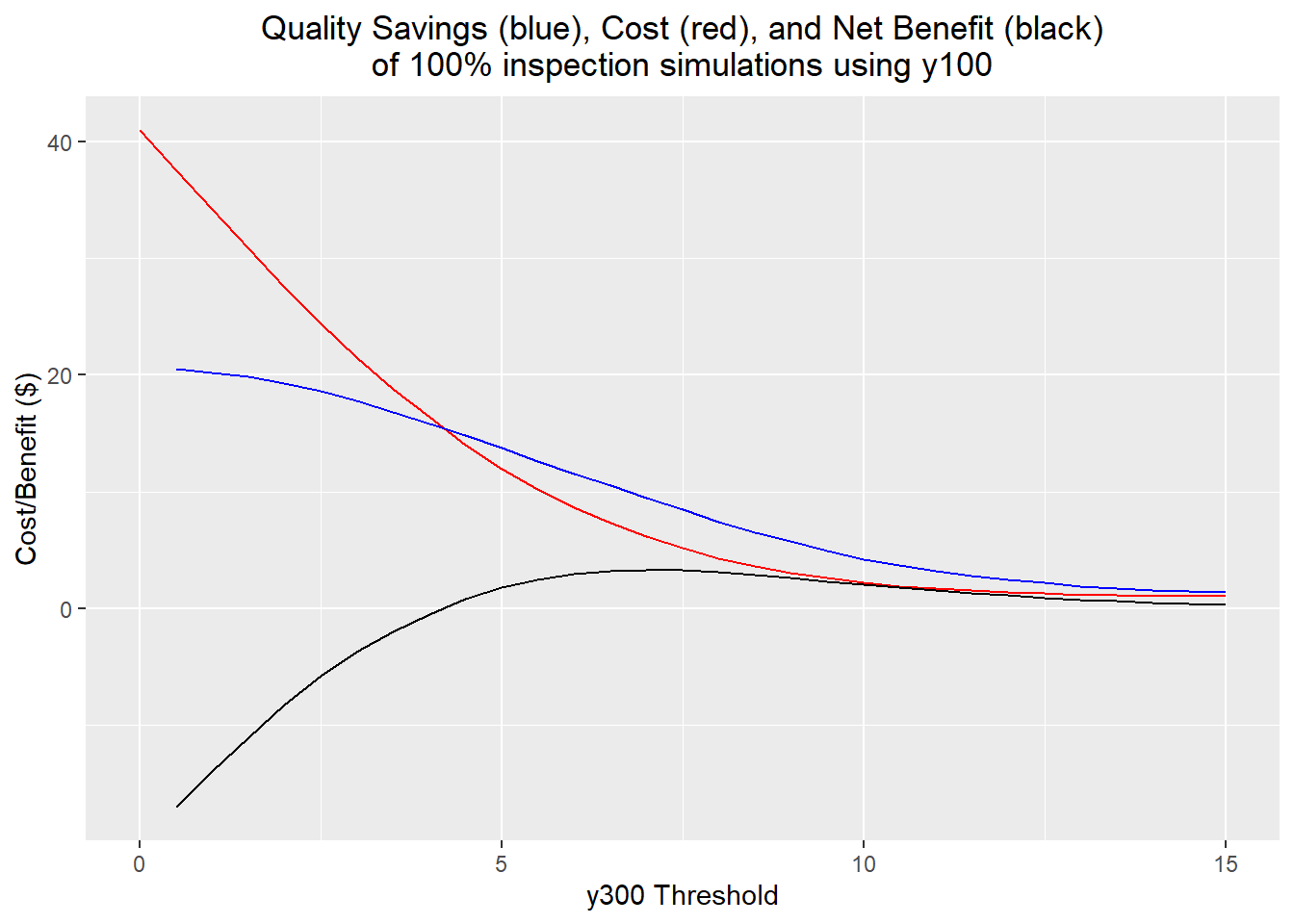
Feedforward Control
Feedback control isn't an option because the output varies substantially between each part, a result of the part-to-part time family of the dominant cause. However, we can measure the dominant cause and apply the adjuster (z1) we identified in the preassembly stage for each part.
We can get a good controller by creating a predictive model for y300, using the linear model for y100 based on x5 and z1, and the y100-y300 model. We can then solve for the optimal adjuster level as a function of x5, using a target y300 of 0. Our predicted output is then \[ \hat y_{300} = 3.059 - 0.971 x_5 + 0.796 z_1 \] The control we apply will then be \[ z_1 = 1.220 x_5 - 3.843 \]
We have one other option for our proportional controller, which is when to activate the controller. There are costs each time we change the value of the adjuster, and costs for using the adjuster increase the further away it is from its default value. It makes sense then that for some values of x5, it may not be worth changing the value of z1 at all. I determined an optimal threshold by using a simulation approach similar to the 100% inspection one.
predicted_out <- function(x5, z1) {
return(-0.971*x5 + 0.796*z1 + 3.059)
}
predicted_out(2.5, 0)## [1] 0.6315predicted_out(3.82, 0)## [1] -0.65022control_func <- function(x5, control.range) {
if (abs(predicted_out(x5, 0)) > control.range)
control <- 1.220*x5-3.843
else
control <- 0
if (control > 13)
control <- 13
if (control < -13)
control <- -13
return(control)
}
control_sim <- function(control.range, n.sims=10000, reset.seed=FALSE) {
z1.vec <- c()
y300.vec <- c()
if (reset.seed)
set.seed(83640)
x5.vec <- rnorm(n.sims, mean=1.78, sd=3.82)
for (i in 1:n.sims) {
control <- control_func(x5.vec[i], control.range)
center <- predicted_out(x5.vec[i], control)
y300 <- center + rnorm(1, mean=0, sd=3.224)
z1.vec <- c(z1.vec, control)
y300.vec <- c(y300.vec, y300)
}
return(data.frame(z1=z1.vec, y300=y300.vec, x5=x5.vec))
}
thresholds <- seq(0, 15, length.out=31)
costs <- c()
quality <- c()
y300.max <- c()
y300.min <- c()
y300.sd <- c()
percent.out <- c()
for (threshold in thresholds)
{
sim <- control_sim(threshold, n.sims=4000, reset.seed=TRUE)
change.cost <- 1.3*mean(sim$z1 != 0)
level.cost <- 0.029*mean(sim$z1^2)
cost.tot <- 0.3 + change.cost + level.cost
quality.cost <- 25 * (1 - (sd(sim$y300)/5)^2)
costs <- c(costs, cost.tot)
quality <- c(quality, quality.cost)
y300.max <- c(y300.max, max(sim$y300))
y300.min <- c(y300.min, min(sim$y300))
y300.sd <- c(y300.sd, sd(sim$y300))
percent.out <- c(percent.out, mean(abs(sim$y300)>10))
}
costs[which.max(quality-costs)]## [1] 2.004331thresholds[which.max(quality-costs)]## [1] 1As expected, the best threshold was quite low, at 1. However, I realized after implementing it that I likely misunderstood how the threshold worked: the control scheme should really change the value of z1 whenever the predicted y300 given the current level of z1 goes above or below the threshold. This misunderstanding likely resulted in an underestimation of the number of changes in the level of z1 during the actual process, underestimating the overall costs of implementation.
ggplot() +
geom_line(aes(x=thresholds, y=quality), color="blue") +
geom_line(aes(x=thresholds, y=costs), color="red") +
geom_line(aes(x=thresholds, y=(quality-costs)), color="black") +
labs(title="Quality Savings (blue), Cost (red), and Net Benefit (black)\nof feedforward control simulations",
x="Threshold",
y="Cost/benefit ($)") +
theme(plot.title=element_text(hjust=0.5))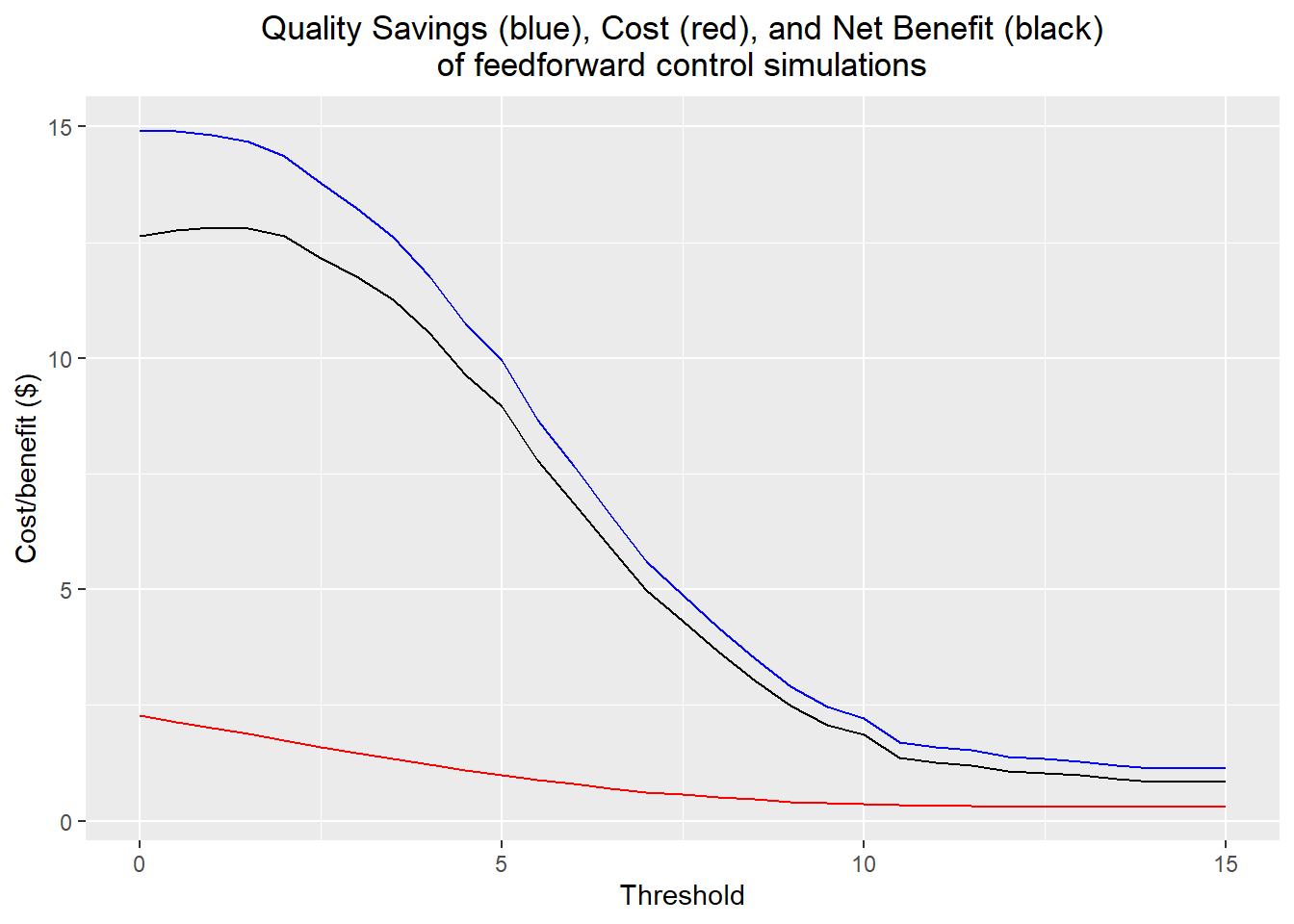
which.max(quality -costs)## [1] 3max(quality -costs)## [1] 12.81455thresholds[which.max(quality -costs)]## [1] 1y300.sd[which.max(quality -costs)]## [1] 3.190786y300.max[which.max(quality -costs)]## [1] 11.19172y300.min[which.max(quality -costs)]## [1] -12.19767percent.out[which.max(quality -costs)]## [1] 0.001Because this appeared to be a particularly promising approach, I simulated the process over a longer period of time and plotted the resulting x5 and y300. We get a process that seems much better behaved, with only 0.1% of parts out of spec, an output standard deviation of 3.19, and a mean and median very close to 0. The x5-y300 plot demonstrates no visible relationship between the dominant cause and the process output.
optim.sim <- control_sim(1, n.sims=4000, reset.seed=TRUE)
mean(abs(optim.sim$y300) > 10)## [1] 0.001c(summary(optim.sim$y300), Std.Dev=sd(optim.sim$y300))## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -12.19766565 -2.15841355 0.03381350 -0.01834995 2.12464523 11.19171740
## Std.Dev
## 3.19078608ggplot() + geom_histogram(aes(x=optim.sim$y300))## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.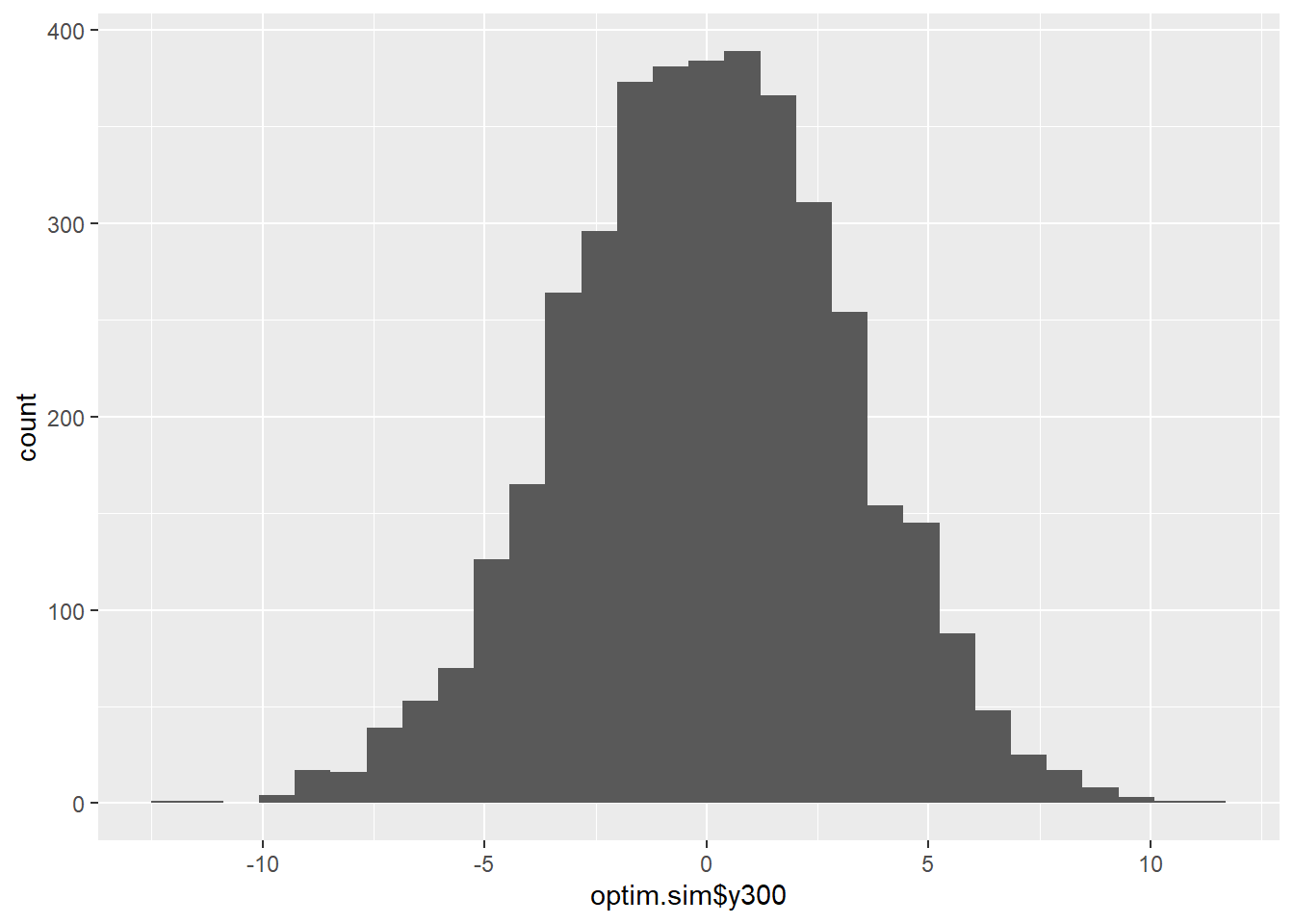
ggplot() + geom_point(aes(x=optim.sim$x5, y=optim.sim$y300), alpha=0.5, shape=16) +
labs(title="Results of feedforward control simulation\nat optimum threshold=1",
x="x5",
y="y300") +
theme(plot.title=element_text(hjust=0.5))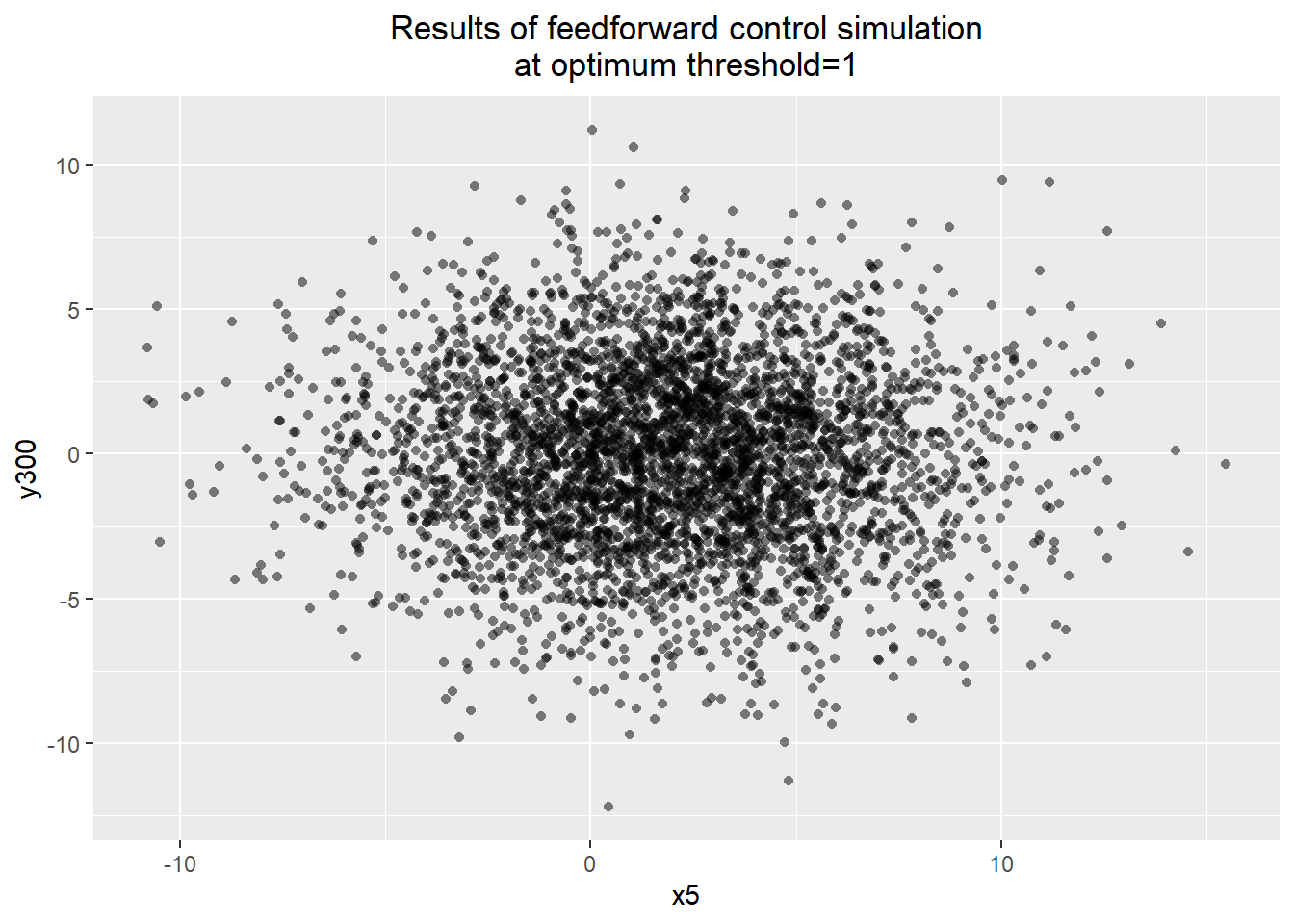
summary(lm(y300 ~ x5, data=optim.sim))##
## Call:
## lm(formula = y300 ~ x5, data = optim.sim)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.2097 -2.1461 0.0193 2.1581 11.1717
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.02087 0.05634 0.370 0.711
## x5 -0.02081 0.01331 -1.563 0.118
##
## Residual standard error: 3.19 on 3998 degrees of freedom
## Multiple R-squared: 0.0006106, Adjusted R-squared: 0.0003607
## F-statistic: 2.443 on 1 and 3998 DF, p-value: 0.1181Desensitization
The last approach to be considered is desensitization. The effect of the desensitizer (z3) was to change the relationship between x5 and y100. From the fitted linear model, the coefficient of x5 was changed from -0.99 to -0.63. Using the estimated standard deviation of 3.82 for x5 obtained from the adjuster investigation, we can estimate the variance through the model: \[ \hat \sigma^2_{y_{100},\text{old}} = (-0.99)^2 \sigma^2_{x_5} + \sigma^2_{\text{resid}} = 18.104 \] \[ \hat \sigma^2_{y_{100},\text{new}} = (-0.63)^2 \sigma^2_{x_5} + \sigma^2_{\text{resid}} = 9.880 \] Or standard deviations are 4.25 and 3.14, respectively. We can then transmit this variance through to y300 using our linear model for y300 based on y100: \(\hat y_{300} = 0.9911 y_{100} - 0.1031\) with a residual standard deviation of 2.095: \[ \hat \sigma^2_{y_{300}, \text{new}} = (0.9911)^2 \sigma^2_{y_{100}, \text{new}} + 2.095^2 = 14.094 \] Or a standard deviation of 3.75. The cost per part is $0.72, while the estimated quality cost savings are $10.91 per part, resulting in a net benefit of $10.19 per part.
Conclusion
The best approach considered was feedforward control, which had a net benefit of $12.81 per part. Surprisingly, the 100% inspection and desensitization approaches also had quite good performance. However, 100% inspection had the somewhat suspect feature of throwing out 80% of the input components, and the desensitization result was based on an estimate of the standard deviation of x5 which was noted to likely be an underestimate. These left no concern about implementing feedforward control.
Validation
After settling on a feedforward approach as described above, the process needed to be checked to make sure it was working as intended. I split this into two phases: a checking phase, where small, inexpensive investigations would be performed to make sure there are no major problems with the new process, and then a new baseline to quantify the gains and set an expectation for how the new process should run.
For the first phase, I started by just measuring the y100 value of a short run of 20 parts. To aid in potential diagnostic measures, I also measured x5. The process immediately appeared to be performing much better, remaining well-centered and having a much lower standard deviation.
val1 <- read.delim("validation-feedforward1.tsv")
c(summary(val1$y100), Std.Dev=sd(val1$y100))## Min. 1st Qu. Median Mean 3rd Qu. Max. Std.Dev
## -3.250000 -1.812500 -0.625000 -0.075000 1.562500 4.500000 2.328457ggplot(data=val1) + geom_point(aes(x=x5, y=y100)) +
labs(title="Plot of y100 vs x5 under feedforward controlled process\n(run 1)") +
geom_hline(yintercept=max(baseline.data$y100)) +
geom_hline(yintercept=min(baseline.data$y100)) +
theme(plot.title=element_text(hjust=0.5))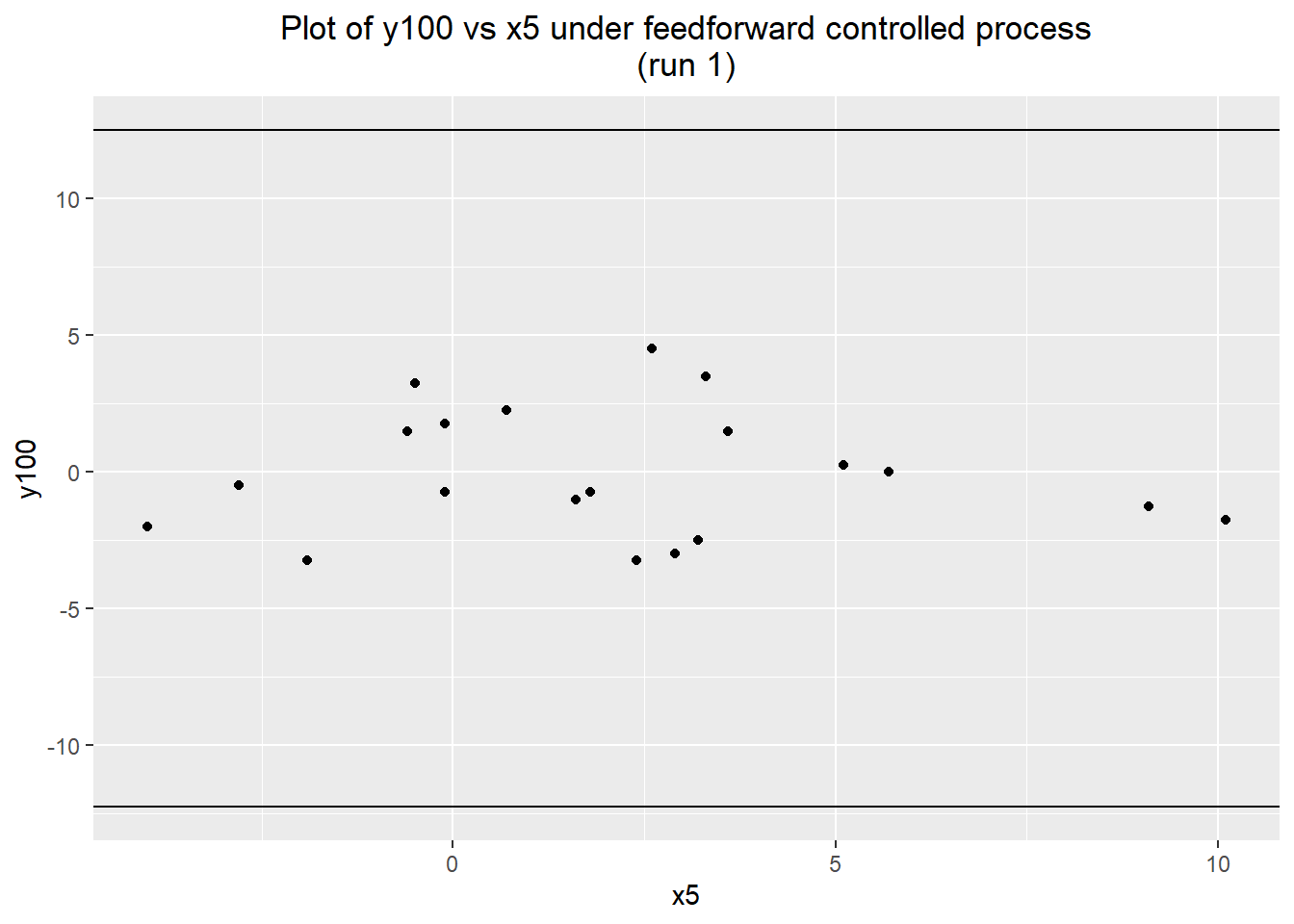
For the second investigation, I moved on to measuring y300. From the observations of y300 in the adjuster investigation, we don't expect there to be any major problems with y300. As expected, the range and standard deviation are a little larger, but the process is still performing quite well.
val2 <- read.delim("validation-feedforward2.tsv")
c(summary(val2$y300), Std.Dev=sd(val2$y300))## Min. 1st Qu. Median Mean 3rd Qu. Max. Std.Dev
## -5.750000 -0.562500 0.875000 0.962500 2.437500 5.500000 2.564016Having seen no problem with the new process, I decided to finish the improvement process with the new baseline. This mirrored the y100 baseline, but was instead applied to y300. Again, according to the setup of the game, we did a baseline investigation for y300, but it's not something I have access to, so the best comparison I can make are against the y100 baseline and the summary statistics of a range in y300 of -12.5 to 12.5 and a standard deviation of 5. Using this baseline, the new process continues to perform much better. The standard deviation is reduced from 5 to 3.06, and no parts are out of spec.
val.final <- read.delim("validation-feedforward-final.tsv")
c(summary(val.final$y300), St.Dev=sd(val.final$y300))## Min. 1st Qu. Median Mean 3rd Qu. Max. St.Dev
## -9.5000000 -2.0000000 0.0000000 -0.1658951 1.7500000 8.2500000 3.0577621ggplot(data=val.final) +
geom_histogram(aes(x=y300), bins=25) +
labs(title="Distribution of y100\npost-feedforward control implementation",
y="Frequency") +
geom_vline(xintercept=-12.5, linetype="dashed") +
geom_vline(xintercept=12.5, linetype="dashed") +
theme(plot.title=element_text(hjust=0.5, face="bold"),
axis.title=element_text(size=12))
val.summary.hour <- data.frame(hour=unique(val.final$partnum%/%60),
y300.mean=tapply(val.final$y300,
val.final$partnum%/%60,
mean),
y300.sd=tapply(val.final$y300,
val.final$partnum%/%60,
sd)
)
start.h <- min(val.final$partnum%/%60)-1
ggplot(data=val.final) +
geom_point(aes(x=partnum/60, y=y300), color="#F06060", alpha=0.7, size=1) +
geom_point(aes(x=hour, y=y300.mean), data=val.summary.hour, color="#2030FF", size=2) +
geom_line(aes(x=hour, y=y300.mean), data=val.summary.hour, color="#2030FF") +
labs(title="Time series of y100 baseline\npost-feedforward control implementation",
x="Hour") +
scale_x_continuous(breaks=seq(start.h, start.h+max(baseline.data$partnum%/%60)+1, 8)) +
geom_hline(yintercept=-12.5) +
geom_hline(yintercept=12.5) +
theme(plot.title=element_text(hjust=0.5, face="bold"),
axis.title=element_text(size=12))
As alluded to in the feedforward control description, the estimate of the implementation costs of feedforward control appeared to be calculated incorrectly. Running the second baseline, the actual implementation cost averaged $5.26 per part. With the reduction in process variation leading to a cost saving of $15.51 per part, this is a net benefit of $10.25 per part. It may be that 100% inspection and desensitization would have been competitive solutions, but what we ended up with is still quite good. Looking back on the implementation, I don't think there is a better solution I could have taken except perhaps better tuning the feedforward control threshold.